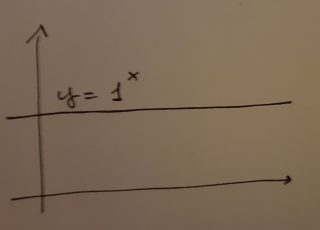Cominciamo dalla definizione di logaritmo, con qualche accenno a esponenziali e funzioni
LOGARITMO DEFINIZIONE: che cos’è un logaritmo???
LA DEFINIZIONE RIGOROSA è la seguente:
il logaritmo in BASE a di un numero x (detto ARGOMENTO DEL LOGARITMO) è l’ESPONENTE da dare alla base per ottenere il numero x.
In parole povere: il LOGARITMO è l’INVERSO dell’elevamento a potenza!
Con le formule:
RICORDA : L’ARGOMENTO DEL LOGARITMO DEVE SEMPRE ESSERE POSITIVO!
X › 0
LA BASE DEVE ESSERE POSITIVA E DIVERSA DA 1:
a › 0 e a ≠ 1
Se x = 1:
log a 1= 0
Infatti qualsiasi numero elevato a zero (e diverso da zero) vale 1
x0 = 1
Facciamo qualche esempio per chiarire il concetto di logaritmo.
NIPOTINI E LOGARITMI: ESEMPI
23 = 8 ⇒ log2 8 = 3
34 = 81 ⇒ log 3 81 = 4
105 = 100000 ⇒ log 10 100000 = 5
NOTA : log2 2 = 1
QUALUNQUE SIA LA BASE : logA A = 1
Infatti
21 = 2 (a1 = a)
LOGARITMO DEFINIZIONE : I LOGARITMI DECIMALI
Se la base è 10, si parla di LOGARITMI DECIMALI O DI BRIGGS E SI SCRIVE:
log 10 x = log
senza indicare la base
LOGARITMI naturali o neperiani:
se la base dei logaritmi è il NUMERO DI NEPERO e = 2.718, si scrive:
log e x = ln
LOGARITMO DEFINIZIONE: la curva logaritmica
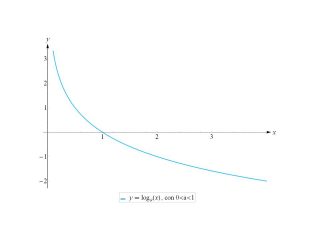
Disegniamo ora il grafico della funzione logaritmo, diverso se la base è maggiore di 1 oppure se è compresa tra 0 e 1.
Se 0‹ a‹ 1:
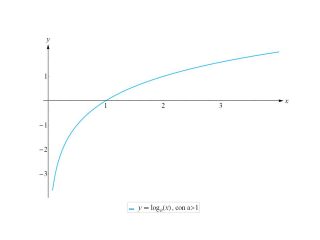
Se a › 1:
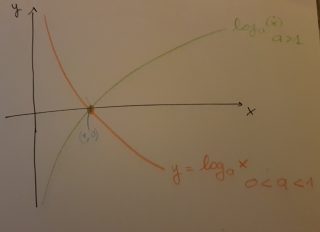
Unendo i due grafici in un unico piano cartesiano:
Domani : le proprietà dei logaritmi !
LOGARITMO DEFINIZIONE: POTENZE, ESPONENZIALI E LOGARITMI.
Il NIPOTINO mi ha chiesto: qual è la differenza tra potenza, esponenziale e logaritmo? Io ho provato a sintetizzare il tutto nella tabella che segue:
In pratica la potenza di un numero è la funzione:
y= x n
dove n è un numero ed è definita qualunque sia il valore di x, positivo o negativo
L’ESPONENZIALE invece è la funzione
y= a x
ed è definito solo per a › 0 e ≠ 1. Infatti se a = 1, otteniamo semplicemente una retta parallela all’asse x:
Infine il logaritmo, come abbiamo visto, è la funzione inversa dell’esponenziale:
y= logax
Fatemi sapere se avete dubbi e volete altri chiarimenti!