Disequazioni scomponibili in fattori

Disequazioni scomponibili in fattori :  come al solito è davvero difficile ritagliarmi un momento da dedicare al blog, che pure dovrebbe essere a cadenza giornaliera. Ma oggi finalmente riesco a trovare la giusta concentrazione per riprendere l’argomento “disequazioni” ed affrontare le disequazioni risolvibili con scomposizioni, che rappresentano una “sintesi” di tutto quello studiato fino ad ora! Infatti per risolverle dovete padroneggiare perfettamente la scomposizione in fattori dei polinomi e naturalmente conoscere l’argomento disequazioni!

Vediamo di che cosa si tratta

Disequazioni scomponibili in fattori : che cosa sono

Non disponendo di formule per la risoluzione di disequazioni ed equazioni di polinomi di grado superiore al secondo, la sola possibilità che abbiamo per risolverle è scomporre il polinomio P(x) in fattori di primo e di secondo grado.

Se abbiamo un polinomio P(x) di grado maggiore di 2, anche le disequazioni del tipo P(x) > 0 o P(x) < 0 sono di grado superiore al secondo. Possiamo però risolverle scomponendo in fattori di primo e secondo grado il polinomio P(x). Una volta scomposto il polinomio, dobbiamo studiare il segno del prodotto di polinomi ottenuto (mediante scomposizione).

Per comprendere meglio vediamo insieme alcuni esempi

Disequazioni scomponibili in fattori : esempi

ESEMPIO 1

Risolviamo la disequazione

x³ − x² ≤ 4x − 4.

Si tratta di una disequazione di TERZO grado, che possiamo però risolvere scomponendola in fattori

PRIMO PASSO : Innanzitutto riportiamo la disequazione in forma normale, trasportando tutti i termini al primo membro, ovviamente cambiati di segno. Otteniamo

x³ − x² − 4x + 4 ≤ 0

SECONDO PASSO:  Scomponiamo il polinomio al primo membro in fattori di PRIMO o SECONDO grado. Raccogliamo x²  tra i primi due termini e -4 tra gli altri due. Otteniamo così

x²(x − 1) − 4(x − 1) ≤ 0

Possiamo ora eseguire un raccoglimento totale :

(x − 1)(x² − 4) ≤ 0

A questo punto potremmo anche scomporre ulteriormente il secondo fattore ma possiamo tranquillamente studiare il segno del binomio di secondo grado. Studiamo il segno dei due fattori:

1° fattore    ⇒       x − 1 > 0 ⇒ x > 1

2° fattore     ⇒      x² − 4 > 0 ⇒ x < −2 ∨ x > 2

Costruiamo la tabella dei segni:

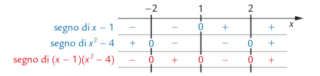
La disequazione (x − 1)(x² − 4) ≤ 0 è soddisfatta quando il prodotto (x − 1)(x² − 4) è negativo o nullo, cioè per:

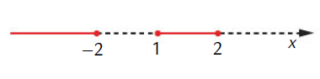
x ≤ − 2 ∨ 1 ≤ x ≤ 2

L’insieme delle soluzioni sulla retta reale è perciò quello evidenziato in rosso nella figura che segue :

Riassumiamo come procedere in generale per risolvere disequazioni scomponibili in fattori e vediamo poi altri esempi

Disequazioni scomponibili in fattori : Procedimento per la risoluzione

• PASSO 1: riconduciamo la disequazione IN FORMA NORMALE (se non lo è già);
• PASSO 2: scomponiamo il polinomio al primo membro della disequazione in fattori di primo o secondo grado (o eventualmente di grado superiore, purché ne sappiamo studiare il segno);
• PASSO 3 : studiamo il segno di ciascun fattore;
• PASSO 4: costruiamo una tabella riassuntiva in cui riportiamo il segno di ciascun fattore. In base alla regola dei segni, ricaviamo il segno del prodotto in ciascun intervallo che si individua;
• PASSO 5: deduciamo dalla tabella l’insieme delle soluzioni della disequazione

RICORDA

1. Possiamo TRASCURARE eventuali fattori sempre positivi, che compaiano nella disequazione ridotta in forma normale e scomposta (non influiscono sul segno del prodotto).

2. Nella costruzione della tabella finale dei segni è importante ordinare correttamente sulla retta  reale gli zeri dei fattori.

3. DOBBIAMO CONSIDERARE il simbolo (>, <, ≥, ≤) che compare nella disequazione solo nell’ultimo passaggio. Infatti la tecnica risolutiva richiede di determinare, SEMPRE E COMUNQUE, lo schema completo del segno dell’espressione e poi dedurre, da tale schema, le soluzioni della disequazione.

Disequazioni scomponibili in fattori : ancora esempi

Vediamo ancora un paio di esempi per meglio comprendere il metodo risolutivo.

Nel pdf allegato trovate la lezione stampabile con molti altri esempi

Disequazioni risolvibili con scomposizioni in fattori

ESEMPIO 2

Risolviamo la disequazione:

x³ − 2x² − 5x + 6 > 0.

Scomponiamo il polinomio

P(x) = x³ − 2x² − 5x + 6

in fattori mediante la regola di Ruffini. Se sostituiamo nel polinomio i divisori del termine noto 6, scopriamo che 1 è uno zero del polinomio.

Ricorda : se un polinomio ha zeri in Z, questi devono essere divisori del termine noto. Perciò i possibili zeri interi del polinomio P(x) sono ±1, ±2, ±3, ±6.

Applichiamo la regola di Ruffini:

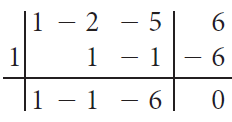
Il nostro polinomio diventa

x³ − 2x² − 5x + 6 = (x − 1)(x² − x − 6).

La disequazione iniziale è quindi equivalente a:

(x − 1)(x² − x − 6) > 0.

Studiamo il segno del polinomio iniziale esaminando il segno dei due polinomi fattori:

x − 1 > 0  per x > 1;

x² − x − 6 > 0.  Applicando la formula risolutiva delle equazioni di secondo grado, troviamo le due radici dell’equazione associata x₁ = -2 e x₂ = 3.

Di conseguenza il polinomio è positivo per valori ESTERNI all’intervallo delle radici, ovvero per x < − 2 ˅ x > 3. L’insieme delle soluzioni sulla retta reale è perciò quello nella figura :

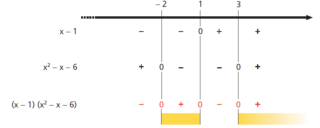
Dal quadro dei segni della figura precedente ricaviamo che la disequazione è verificata per

  − 2 < x < 1 ˅ x > 3, ossia S= ]− 2; 1[∪]3; +3[.

ESEMPIO 3

Risolviamo la disequazione biquadratica:

x⁴ − 13x² + 36 ≥ 0.

L’equazione associata :   x⁴ − 13x² + 36 = 0 è un’equazione biquadratica. Per risolverla, introduciamo l’incognita ausiliaria z e poniamo x² = z:

z² − 13z + 36 = 0 per z₁ = 4, z₂ = 9

RICORDA: In generale, un’equazione biquadratica nell’incognita x è riconducibile alla forma:

ax⁴ + bx² + c = 0, a ≠0.

La disequazione di quarto grado, nell’incognita x, è quindi equivalente alla disequazione di secondo grado, nell’incognita ausiliaria z. Otteniamo

z² − 13z + 36  ≥  0 per z ≤ 4 ˅ z ≥ 9,

da cui

x⁴ − 13x² + 36 ≥ 0 per x² ≤ 4 ˅ x² ≥ 9,

ossia:

    (− 2 ≤ x ≤ 2) ˅ (x ≤ − 3 ˅ x ≥ 3).

S =  (-∞, -3]∪[-2, +2] ∪ [+3. +∞)

Disequazioni scomponibili in fattori : GLI ERRORI DA EVITARE

1)MAI SEMPLIFICARE I DUE MEMBRI DI UNA DISEQUAZIONE PER UN FATTORE DI CUI NON CONOSCIAMO IL SEGNO

Ad esempio

2) OGNI FATTORE della disequazione deve avere la PROPRIA RETTA: non dobbiamo MAI riportare su due rette diverse i segni dello stesso fattore

Ad esempio, risolvendo la disequazione

(x-1) (x²-4) >0

troviamo che

x-1>0 se x>1

(x²-4) >0  se x<-2 ˅ x > 2

OSSERVIAMO BENE LE TABELLE DEI SEGNI

 

3) Come già detto, se la disequazione è FRAZIONARIA, dopo aver calcolato il DENOMINATORE COMUNE e aver svolto i calcoli, NON DOBBIAMO MAI ELIMINARE I DENOMINATORI che contengono l’incognita, se non DOPO averne studiato il segno. Ad esempio:

4) Nel caso in cui nel verso di una disequazione FRAZIONARIA sia COMPRESO anche il SEGNO DI UGUAGLIANZA, il simbolo va messo NELLO STUDIO DEL NUMERATORE MA NON IN QUELLO DEL DENOMINATORE. Ad esempio

Disequazioni scomponibili in fattori :Bibliografia

• Gabriella Cariani, Mariapia Fico, Salvatore Mattina, Ileana Pelicioli- Matematica c.v.d. Calcolare, valutare, dedurre. Ediz. blu– Loescher editore, 2019
• Sasso, C. Zanone – I colori della matematica  – Petrini
• Bergamini, G. Barozzi, A. Trifone : Matematica blu 2.0 – Zanichelli

Disequazioni scomponibili in fattori : per saperne di più

• DISEQUAZIONI DI SECONDO GRADO
• Disequazioni monomie
• Disequazioni binomie
• disequazioni trinomie
• Studio di equazioni e disequazioni
• DISEQUAZIONI LETTERALI O PARAMETRICHE
• TIPI DI DISEQUAZIONI
• DISEQUAZIONI RICONDUCIBILI AL PRIMO GRADO
• DISEQUAZIONI ESEMPI SVOLTI
• DISEQUAZIONI : che cosa sono
• DISEQUAZIONI DI PRIMO GRADO INTERE
• GLI INTERVALLI
• TIPI DI INTERVALLI