Nelle lezioni precedenti abbiamo imparato che cosa sono le disequazioni (vedi QUI) ed abbiamo approfondito un pochino le disequazioni di primo grado intere.
Vediamo ora altri esempi per capire meglio l’argomento
DISEQUAZIONI ESEMPI SVOLTI : Come si risolve una disequazione intera?
Ricapitoliamo insieme come procedere per la risoluzione di una disequazione intera, in cui l’incognita COMPARE SOLO AL NUMERATORE.
Per risolvere una disequazione intera la devo trasformare, applicando i due principi di equivalenza, in una disequazione equivalente nella forma
ax < b oppure ax > b
Partendo dalla disequazione data, quindi procediamo nel modo seguente :
- eliminiamo le parentesi, eseguendo le operazioni indicate
- riduciamo allo stesso denominatore ( minimo comune multiplo tra i denominatori) i due membri della disequazione ed eliminiamo il denominatore così ottenuto (regola della moltiplicazione)
- spostiamo i termini con l’incognita a primo membro e i termini noti a secondo membro, applicando la regola del trasporto (ovvero cambiando il segno ai termini che spostiamo!!!)
- se il coefficiente dell’incognita è negativo, moltiplichiamo per -1, cambiando il verso della disequazione (regola della moltiplicazione).
- A noi non interessa trovare -x ma il valore di x!!!
- dividiamo entrambi i membri della disequazione per il coefficiente dell’incognita (regola della divisione)
- Scriviamo poi la soluzione ottenuta
- per caratteristica
- graficamente
- simbolicamente con gli intervalli
DISEQUAZIONI ESEMPI SVOLTI.
Esempio 1
Risolviamo la seguente disequazione
x + 4 − 3 ( x − 3 ) ≥ 5 − ( 2 + 7 x )
Eliminiamo le parentesi, eseguendo le operazioni indicate:
x + 4 – 3x + 9 ≥ 5 – 2 – 7x
Applichiamo ora la regola del trasporto, cambiando di segno ai termini che spostiamo da un membro ad un altro
x– 3x + 7x ≥ 5 – 4 – 9 – 2
Sommiamo ora i termini simili:
5x ≥ -10
Dividiamo entrambi i membri per il coefficiente di x (in questo caso 5)
x ≥ -10/5
Otteniamo x ≥ – 2 (soluzione per caratteristica)
Graficamente :

Con gli intervalli : S = [-2 ; + ∞)
Esempio 2 :
x ( x – 3 )+ 2 ( 3 – x ) ≤ ( x+ 1)2 – 4 x
X2 – 3X + 6 – 2X ≤ X2 + 2X + 1 -4X
-3X +4X -2X ≤ -6+1
-X ≤ -5
Siccome l’incognita è negativa, moltiplico tutto per -1 e giro il verso della disequazione
otteniamo
x ≥ 5
Graficamente :

Ovvero:
S = [ 5 ; + ∞)
Esempio 3




Esempio 4

Calcoliamo il m.c.d., che è 6 :
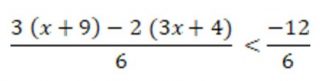
Eliminiamo i denominatori ed eseguiamo le operazioni indicate

Sommando i termini simili e applicando la regola del trasporto, otteniamo

Moltiplicando entrambi i membri per – 1:

Dividendo per il coefficiente di x, infine, abbiamo la nostra soluzione:

In forma grafica:

Ovvero:
S = (31/3 ; + ∞)
Vedremo nelle prossime lezioni come risolvere le disequazioni riconducibili ad un prodotto di fattori di primo grado, le disequazioni intere letterali, i sistemi di primo grado e le disequazioni fratte.