Disequazioni binomie : definizione
Si chiamano binomie le disequazioni che si possono ricondurre a una delle seguenti forme, con a ≠ 0, b ≠ 0 ed n ∊ N – {0}:
axn + b < 0 oppure axn + b ≤ 0
axn + b > 0 oppure axn + b ≥ 0
NOTA BENE : per b = 0 la disequazione diventa monomia
Come nel caso delle monomie, anche la risoluzione delle binomie cambia a seconda che n sia pari o dispari. Vediamo come procedere nei due casi
Disequazioni binomie : n DISPARI
Se n è dispari, ricordiamo che una disuguaglianza tra due numeri reali equivale a quella nello stesso verso tra le loro radici n-esime. Cioè
![]()
Tenendo conto di questa proprietà, la risoluzione di una disequazione binomia con n dispari si può effettuare facilmente.
VEDIAMO ALCUNI ESEMPI
ESEMPIO 1
Risolviamo la disequazione
3x5 + 1 > 0
Possiamo scrivere :
3x5 > -1
Da cui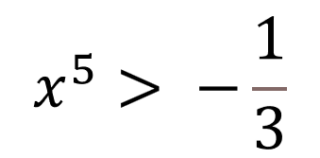
Estraendo la radice quinta da entrambi i membri otteniamo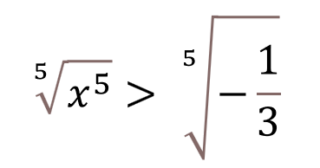
Semplificando indice della radice ed esponente al primo membro, ricaviamo la soluzione cercata:
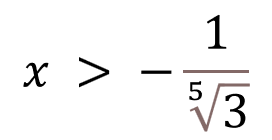
ESEMPIO 2
Proviamo ora a risolvere la seguente disequazione
− 8x3 + 1 > 0
Si tratta di una disequazione binomia con esponente dispari. Come nel caso precedente possiamo scrivere
− 8x3 > -1
Ovvero, cambiando il segno dei due termini e invertendo il verso della disuguaglianza
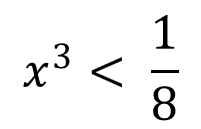
Estraendo la radice cubica da entrambi i membri e ricordando che 8 = 2³ otteniamo:
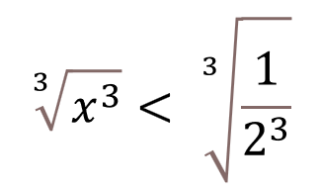
Ovvero la soluzione richiesta :
x < 1/2
Disequazioni binomie : n pari
Se n è pari, la risoluzione di una disequazione binomia è immediata oppure possiamo effettuarla facilmente mediante la sostituzione
xn/2 = t
Vediamo subito come procedere con alcuni esempi nel caso in cui l’esponente dell’incognita sia pari
ESEMPIO 1 (n pari)
Risolviamo la seguente disequazione
10x4 + 1 > 0
Il primo membro è sempre positivo, essendo la somma di un termine, 10x4, sempre non negativo, e di 1. Di conseguenza la disequazione è verificata per ogni x ∊ R.
ESEMPIO 2 (n pari)
Proviamo ora a risolvere la disequazione
100x4 − 1 ≥ 0
Poniamo
x2 = t
Di conseguenza x4 = t2
Effettuando le opportune sostituzioni, otteniamo la seguente disequazione in t:
100 t2 − 1 ≥ 0
Scomponendo come differenza di due quadrati, otteniamo
(10 t – 1) (10t +1) ≥ 0
Da cui ricaviamo la soluzione
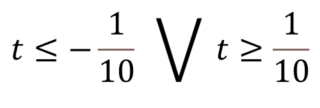
Siccome
t = x2
possiamo concludere che la disequazione originaria è soddisfatta per i valori di x per cui risulta
 ESEMPIO 3 (n pari)
ESEMPIO 3 (n pari)
Risolviamo ora la seguente disequazione
−x4 + 16 ≥ 0
Come nell’esempio precedente, poniamo x2 = t. Risulta x4 = t2 e, sostituendo, otteniamo la seguente disequazione in t, che risolviamo:
− t² + 16 ≥ 0 ⇒ t2 − 16 ≤ 0 ⇒ −4 ≤ t ≤ 4
Ricordando che t = x2, concludiamo che la disequazione originaria è soddisfatta in corrispondenza dei valori di x per cui:
−4 ≤ x2 ≤ 4
Osserviamo che è sempre −4 ≤ x2 (essendo un quadrato sempre positivo o nullo), quindi la relazione precedente equivale a x2 ≤ 4, ovvero per
−2 ≤ x ≤ 2.
ESEMPIO 4 (n pari)
Consideriamo la seguente disequazione :
2x6 +√2 ≤ 0
Il primo membro è sempre positivo, essendo la somma di due termini sempre positivi, quindi la disequazione non è soddisfatta da alcun valore reale di x.
Disequazioni binomie : ricapitolando
In pratica, per le disequazioni binomie otteniamo i seguenti schemi risolutivi
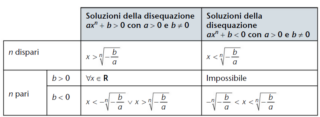
Disequazioni binomie : Bibliografia
- Gabriella Cariani, Mariapia Fico, Salvatore Mattina, Ileana Pelicioli- Matematica c.v.d. Calcolare, valutare, dedurre. Ediz. blu– Loescher editore, 2019
- Sasso, C. Zanone – I colori della matematica – Petrini
- Bergamini, G. Barozzi, A. Trifone : Matematica blu 2.0 – Zanichelli
Disequazioni binomie : per saperne di più
- DISEQUAZIONI DI SECONDO GRADO
- Disequazioni monomie
- Studio di equazioni e disequazioni
- DISEQUAZIONI LETTERALI O PARAMETRICHE
- TIPI DI DISEQUAZIONI
- DISEQUAZIONI RICONDUCIBILI AL PRIMO GRADO
- DISEQUAZIONI ESEMPI SVOLTI
- DISEQUAZIONI : che cosa sono
- DISEQUAZIONI DI PRIMO GRADO INTERE
- GLI INTERVALLI
- TIPI DI INTERVALLI