Infatti ho intrapreso diverse collaborazioni con varie scuole ed università ma ho anche deciso di realizzare un desiderio e prendermi una laurea in Lettere Classiche! Così anch’io sono tornata a scuola…
Ma a tenermi impegnata sono soprattutto le lezioni di matematica, chimica e fisica, oltre a quelle di latino e greco. Insomma, se riuscirò a realizzare i miei progetti, avremo tantissimo da lavorare!
Oggi riprendiamo con la matematica, con quella che è stata la “lezione di apertura” di quest’anno scolastico!
LE EQUAZIONI LETTERALI : che cosa sono
Ricordate che cos’è un’equazione?
Un’equazione è un’uguaglianza fra due espressioni letterali per la quale ci chiediamo se esistono valori che, sostituiti a una o più lettere, la rendono vera

Le equazioni letterali sono equazioni in cui, oltre all’incognita, compaiono anche altre lettere, dette parametri, che sono valori reali costanti.
Le soluzioni dell’equazione dipendono dal valore che assumono i coefficienti letterali dell’incognita. La risoluzione prende il nome di discussione in quanto è necessario discutere i valori che assumono i parametri per determinare l’insieme delle soluzioni.
Le equazioni letterali presentano una o più lettere oltre all’incognita
Vediamo ora come si procede per la risoluzione di queste equazioni, nel caso in cui siano intere oppure frazionarie
Risolvere un’equazione letterale intera
Data un’equazione letterale di primo grado, non dobbiamo soltanto risolverla ma bisogna anche discuterla, cioè studiare, al variare dei parametri, quando l’equazione è determinata, indeterminata o impossibile.
Nella soluzione delle equazioni letterali intere è necessario discutere per quali valori delle lettere presenti l’equazione è determinata, indeterminata o impossibile
Iniziamo con le equazioni letterali INTERE, in cui l’incognita compare solo al numeratore
ESEMPIO
Risolviamo l’equazione, nell’incognita x:
ax -3a =2x.
- Portiamo al primo membro i termini con l’incognita e al secondo gli altri, riconducendo così l’equazione alla sua forma normale
ax-2x =3a.
- Raccogliamo ora la x:
(a -2)x =3a.
-
Discussione
PRIMA di dividere i due membri per (a -2) dobbiamo porre la condizione:
a -2≠ 0, ossia a ≠ 2.
Se questa condizione è verificata, possiamo dividere i due membri per a – 2. In tal caso l’equazione è determinata e la soluzione è:

Dobbiamo ora analizzare il caso a =2.
Sostituiamo 2 ad a nell’equazione
(a -2)x =3a.
Troviamo:
0x =3 ∘ 2 → 0x = 6 → l’equazione è impossibile.
Ricapitolando:
- se a ≠ 2, l’equazione è determinata e la soluzione è
- se a =2, l’equazione è impossibile
Nel pdf allegato troverete molti altri esempi
IN SINTESI : PROCEDIMENTO PER LA DISCUSSIONE DI UN’EQUAZIONE LETTERALE INTERA DI PRIMO GRADO NELL’INCOGNITA x
PASSO 1: Se necessario, riportiamo l’equazione alla forma normale Ax = B
PASSO 2 : Risolviamo l’equazione ottenuta e la discutiamo.
- Determiniamo i valori dei parametri per cui A ≠ 0: per tutti questi valori l’equazione è DETERMINATA e ne calcoliamo la soluzione
- Esaminiamo le equazioni che si ottengono per A = 0. Per questi valori, l’equazione è IMPOSSIBILE oppure INDETERMINATA
PASSO 3 : riassumiamo le conclusioni ottenute al passo precedente
RISOLUZIONE DI UN’EQUAZIONE LETTERALE FRATTA
Vediamo ora come dobbiamo procedere nel caso di un’equazione letterale in cui compaiono incognite e/o parametri ai denominatori.
Anche nella soluzione delle equazioni letterali fratte è necessaria la discussione.
ESEMPIO
Risolviamo la seguente equazione, nell’incognita x:
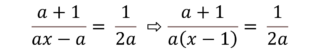
Dobbiamo innanzitutto imporre che i denominatori siano non nulli (condizioni di esistenza):
- a(x-1)≠ 0 ⇨ a ≠ 0 ⋀ x≠ 1
- 2a ≠ 0 ⇨ a ≠ 0
Calcoliamo quindi il minimo comune multiplo dei denominatori (m.c.d.) :

Moltiplicando entrambi i membri dell’equazione per il m.c.d., otteniamo un’equazione intera:
2a+2 = x -1
Ovvero, riportando al primo membro il termine con la x e al secondo tutti gli altri:
x = 2a+ 3
Per le condizioni di esistenza deve essere x≠ 1 ovvero
2a+ 3 ≠ 1 ⇨ a ≠ -1
Per a = -1, l’equazione è impossibile.
RICAPITOLANDO
- se a = 0, l’equazione perde di significato;
- se a = – 1, l’equazione è impossibile;
- se a ≠ 0 ⋀ a≠ -1, l’equazione è determinata e la soluzione è x=2a+3
IN SINTESI : PROCEDIMENTO PER LA DISCUSSIONE DI UN’EQUAZIONE LETTERALE CON INCOGNITE E/O PARAMETRI AL DENOMINATORE
PASSO 1 : Se l’equazione letterale è frazionaria oppure contiene parametri anche al denominatore, dobbiamo innanzi tutto porre le CONDIZIONI DI ESISTENZA delle frazioni algebriche presenti. Esse sono di due tipi
- condizioni sui parametri: escludono i valori per cui l’equazione perde significato
- condizioni sulle incognite: vanno poi riprese alla fine per verificare l’accettabilità delle soluzioni
PASSO 2 : Dobbiamo ora ricondurre l’equazione alla forma INTERA, moltiplicando entrambi i membri per il minimo comune multiplo dei denominatori. Risolviamo poi e discutiamo l’eguazione ottenuta
PASSO 3 : Se al passo 1 abbiamo posto delle condizioni sulle incognite, dobbiamo discutere L’ACCETTABILITÀ delle soluzioni in relazione a tali condizioni
PASSO 4: riassumiamo i risultati ottenuti
Nel pdf allegato troverete altri esempi di risoluzione di un’equazione letterale frazionaria
EQUAZIONI LETTERALI O PARAMETRICHE
Equazioni letterali e formule
In molte discipline scientifiche (fisica, chimica, economia, ecc.) incontriamo spesso delle formule, espresse sotto forma di uguaglianze, che esprimono relazioni tra grandezze rappresentate da variabili.
E spesso dobbiamo esprimere una grandezza in funzione delle altre. Per comodità, possiamo interpretare le formule come equazioni letterali in cui l’incognita è rappresentata dalla grandezza che si vuole esprimere
In pratica: quando ricaviamo le “formule inverse”, dobbiamo risolvere delle equazioni letterali. Nel pdf alcuni esempi.
Riassumendo :
a ≠1⇨ equazione determinata :
a= 1 ⇨ equazione indeterminata
Risolvi e discuti le seguenti equazioni letterali
- ax = x+a (a ≠1 x =a/(a-1) // a = 1 imposs)
- 6x -3 (x + 2a) = a+4(x-2a) [x=a]
- 2x -4(3x-a) = 6(a-2x) + 6a [x=4a]
- (a2-3a)x = a (a2-9) (a ≠0 ⋀ a ≠ 3 : x = a + 3 ; a = 0, a = 3 : indet)
- a(5-4x)= 4+ a2 (1-x) (a ≠0 ⋀ a ≠ 4 : x = (a -1)/a ; a = 0 : imposs; a = 4 : indet)
- 2[3 + (a+3)x] + 2ax = 3-3(2x-1) (a ≠ -3 : x = 0 ; a = -3 : indet)