Oggi cominciamo un nuovo argomento, legato alla Geometria. Siccome i miei ragazzi avevano bisogno di una serie di esercizi di RIPASSO, cominceremo da una parte pratica e poi passeremo alla teoria.
Il mio “progetto” è cominciare dalle basi, perché ho notato che molti dei miei ragazzi hanno difficoltà proprio con la Geometria, che è sempre stata la parte della Matematica da me preferita…
Ricordiamo intanto alcune definizioni. A fine pagina trovate il pdf con le formule utili
AREA DEI POLIGONI ESERCIZI: che cos’è l’area delle figure piane
La misura della parte di piano occupata da un poligono, cioè la misura della sua superficie, si chiama area.
RICORDA: per misurare l’estensione di una superficie, dobbiamo confrontarla con un’unità di misura scelta come riferimento, così da stabilire quante volte essa è contenuta in quella da misurare.
Nel Sistema Internazionale, l’unità di misura della superficie è il m²
EQUIVALENZA DI FIGURE PIANE : definizione
Due superfici che hanno la stessa AREA si dicono equivalenti. Indichiamo l’equivalenza fra superfici con il simbolo ≐
EQUIVALENZA DI FIGURE PIANE : PROPRIETA’
L’equivalenza tra superfici piane gode delle proprietà riflessiva, simmetrica e transitiva.
- Proprietà riflessiva:
Ogni superficie piana è equivalente a se stessa
- Proprietà simmetrica
Se una superficie S è equivalente a una superficie S’, allora anche S’ è equivalente a S
- Proprietà transitiva
Se una superficie S è equivalente a una superficie S’ e S’ è equivalente a una superficie T, allora anche S è equivalente a T
Valgono inoltre i seguenti ASSIOMI
- Poligoni congruenti sono equivalenti.
- Un poligono non è equivalente ad una sua parte propria.
- Somma e differenza di poligoni equivalenti originano poligoni equivalenti.
Postulato di De Zolt
Una superficie non può essere equivalente a una sua parte.
AREA DEI POLIGONI ESERCIZI
Ed ora è il momento di metterci al lavoro! Vi propongo una serie di esercizi molto semplici, per prendere poco a poco confidenza con l’argomento “risoluzione dei problemi“.
AREA DEI POLIGONI : IL QUADRATO
Ricordiamo che il quadrato è un poligono regolare con quatto lati e quattro angoli uguali, per il quale valgono le seguenti formule :
- P = 4 𝑙
- A = 𝑙 ∘ 𝑙
ESERCIZIO 1
Calcola l’area di un quadrato che ha il perimetro di 60 cm
RISOLUZIONE
Sappiamo che il perimetro del quadrato si ottiene moltiplicando per 4 la lunghezza di un suo lato. Siccome per calcolare l’area ci serve questo dato, ricaviamo la lunghezza del lato:
𝑙 = P : 4 = 60 : 4 = 15 cm
L’area vale quindi:
A = 𝑙 ∘ 𝑙 = 15 ∘15 = 225 cm2
ESERCIZIO 2
Calcola il perimetro di un quadrato che ha l’area di 784 cm2.
RISOLUZIONE
Per risolvere il problema abbiamo bisogno di conoscere la lunghezza del lato del quadrato. Sappiamo però che l’area di un quadrato si ottiene moltiplicando il lato per se stesso. Possiamo quindi ricavare la lunghezza del lato:
𝑙 =√ A = √784 = 28 cm
A questo punto possiamo calcolare facilmente il perimetro richiesto:
P = 4 ∘ 𝑙 = 28 ∘ 4 = 112 cm
AREA DEI POLIGONI : I RETTANGOLI
Il rettangolo è un quadrilatero con quattro angoli retti e i lati uguali e paralleli due a due. Valgono le formule seguenti:
- P = (b+h) * 2
- A = b * h
ESERCIZIO 1
I terreni di gioco per la Lega Nazionale Professionisti italiana di calcio devono avere le dimensioni obbligatorie di m 105 x 68. E’ tollerata, per il lato corto, la dimensione minima di m 65 nei soli casi di comprovate difficoltà tecniche dell’impianto.
Calcola la differenza tra le due superfici e tra i perimetri dei due casi.
SVOLGIMENTO
Dobbiamo applicare semplicemente le formule per il calcolo del perimetro e dell’area di un rettangolo.
Sappiamo infatti che :
P = (b + h) x 2
A = b x h
Con i valori numerici dati abbiamo
A1 = 105 ∘ 68 = 7140 m²
P1 = (105 + 68)∘ 2 = 346 m
A2 = 105 ∘ 65 = 6825 m²
P2 = (105 + 65)∘ 2 = 340 m
Risulta quindi :
- A1 – A2 = 7140 – 6825 = 315 m²
- P1 – P2 = 346 – 340 = 6 m
ESERCIZIO 2
Calcola il perimetro di un rettangolo che ha l’area di 288 cm² e l’altezza di 16 cm.
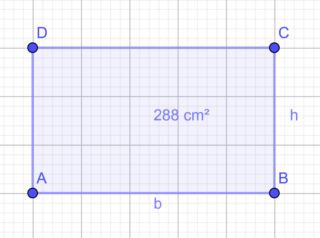DATI
h = 16 cm
A = 288 cm²
P = ?
Siccome il perimetro si calcola secondo la formula:
P = (b + h) x 2
per poterlo calcolare dobbiamo ricavare la lunghezza della base.
Sappiamo però che :
A = b x h
per cui, applicando la formula inversa possiamo calcolare la base :
b = A : h = 288 : 16 = 18 cm
Calcoliamo ora il perimetro:
P = (b + h) x 2 = (18 + 16) x 2 = 68 cm
ESERCIZIO 3
In un rettangolo la differenza delle due dimensioni è pari a 40 cm. Calcola la misura del perimetro e dell’area del rettangolo sapendo che una dimensione è i 3/5 dell’altra.
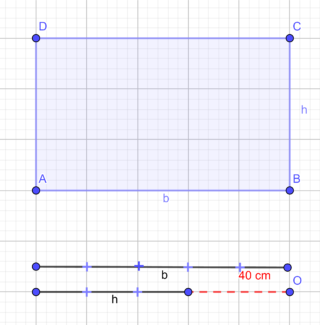DATI
b-h = 40cm
h = 3/5 b
A = ?
P = ?
Sappiamo che, nota la differenza tra due numeri e il loro rapporto, possiamo ricavare velocemente il loro valore. Come si vede dal disegno, infatti la differenza tra i due numeri equivale ai 2/5. Per trovare quanto vale un pezzettino, dobbiamo calcolare il valore di quella che si chiama “unità frazionaria”, dividendo per 2 (che è anche la differenza tra numeratore e denominatore della frazione di partenza):
u.f. = 40 : 2 = 20 cm
Adesso ci basta moltiplicare per il numeratore e poi per il denominatore per trovare altezza e base:
- h = 20 x 3 = 60 cm
- b = 20 x 5 = 100 cm
Ora ci resta solo da determinare perimetro ed area:
- P = (100 + 60) x 2 = 320 cm
- A = (b x h) = 100 x 60 = 6000 cm²
ESERCIZIO 4
In un rettangolo la differenza delle lunghezze delle due dimensioni misura 5 cm ed una è i 4/3 dell’altra. Calcola la misura dell’area e il perimetro del rettangolo.
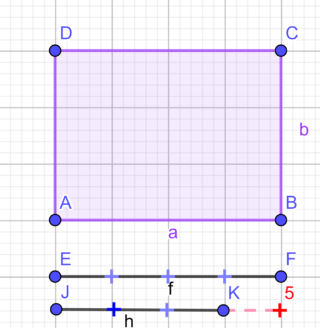DATI
b – h = 5 cm
a = 4/3 b
A = ?
P = ?
RISOLUZIONE
Come nel problema precedente, calcoliamo il valore della cosiddetta “unità frazionaria”, che questa volta è proprio pari alla differenza tra base e altezza. Ci basta quindi moltiplicare una volta per numeratore e denominatore per trovare b ed h e poi ricavare il valore di perimetro ed area. Abbiamo:
b = 5 x 4 = 20 cm
h = 5 x 3 = 15 cm
- P = (b + h) x 2 = (20 + 15) x 2 = 70 cm
- A = b x h = 20 x 15 = 300 cm²
AREA DEI POLIGONI : PARALLELOGRAMMA
I parallelogrammi sono quadrilateri che hanno due coppie di lati paralleli. A differenza dei rettangoli, però, gli angoli non sono retti. Anche in questo caso, risulta:
- P = (b+h) * 2
- A = b * h
ESERCIZIO 1
Un parallelogramma ha la base di 40 cm e l’altezza di 38 cm. Trova la sua area.
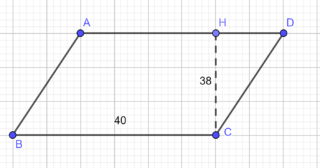DATI
b = 40 cm
h = 38 cm
A = ?
Siccome :
A = b x h
disponiamo di tutti i dati per calcolare l’area del parallelogramma :
A = 40 x 38 = 1520 cm²
ESERCIZIO 2
In un parallelogramma la base misura 24 cm e l’area è di 360 cm². Calcola l’altezza del parallelogramma.
DATI
b = 24 cm
A = 360 cm²
h = ?
Siccome
A = b x h
per calcolare l’altezza h ci basta applicare la formula inversa:
h = A : b
ovvero, con i dati numerici forniti
h = 360 : 24 = 15 cm
AREA DEI POLIGONI : ROMBO
Nel rombo tutti i lati sono uguali tra loro e paralleli 2 a 2. Inoltre gli angoli opposti sono uguali tra loro. Le diagonali hanno lunghezze diverse e, incrociandosi, si tagliano a metà, formando 4 angoli retti (cioè
sono perpendicolari tra loro).
Risulta:
P = 4 ∘ 𝓁
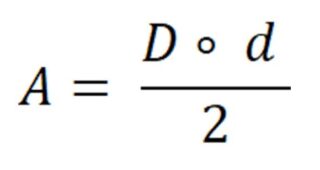
ESERCIZIO 1
Un rombo ha le due diagonali che misurano rispettivamente 6 cm e 8 cm e il lato obliquo di 5 cm. Calcola il perimetro e l’area del rombo.
DATI
- AB = 8 cm = D
- CD = 6 cm = d
- AD = 5 cm = 𝓁
- A = ?
- P = ?
RISOLUZIONE
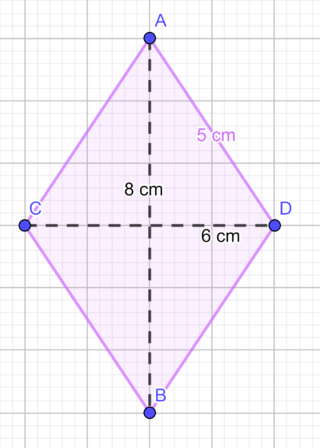
Per il rombo valgono le seguenti formule :
P = 4 ∘ 𝓁
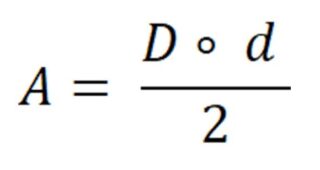
Disponiamo quindi di tutti i dati che ci servono per risolvere il problema. Ci basta perciò sostituire i valori forniti nelle formule scritte:
P = 4 ∘ 5 = 20 cm
A = 24 cm²
ESERCIZIO 2
Un rombo ha le una delle due diagonali che misura 15 cm e l’area di 150 cm². Calcola la misura dell’altra diagonale.
DATI
- AB = 15 cm = D
- A = 150 cm²
- CD = ?
RISOLUZIONE
Siccome :
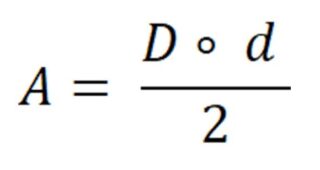
per calcolare la diagonale mancante ci basta applicare la formula inversa:
Con i dati numerici abbiamo :
D = (2x 150) : 15 = 20 cm
AREA DEI POLIGONI : trapezi
Il trapezio è un quadrilatero con due soli lati paralleli. Tali lati paralleli sono necessariamente opposti e vengono chiamati basi del trapezio (in particolare base maggiore e base minore).
Risulta:
ESERCIZIO 1
Calcola la misura del perimetro e dell’area di un trapezio rettangolo ABCD, rettangolo in A, sapendo che le due basi misurano 4 cm e 8 cm, l’altezza 2 cm e il lato obliquo 2,5 cm.
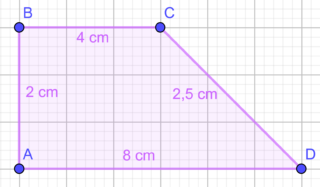
DATI
- AD = Base maggiore = B = 8 cm
- BC = base minore = b = 4 cm
- AB = altezza = h = 2 cm
- CD = 2,5 cm
- A = ?
- P = ?
RISOLUZIONE
Scriviamo le formule per il calcolo di area e perimetro del trapezio:
P = AD + CD + BC + BA
Disponiamo quindi di tutti i dati che ci servono per risolvere il problema. Risulta:
- P = 8+ 4+2.5+2 = 16,5 cm
- A = [(8+4)∘ 2] : 2 = 12 cm²
ESERCIZIO 2
Calcola la misura delle basi di un trapezio isoscele ABCD di 144 cm² la cui altezza misura 6 cm, sapendo che la differenza tra le basi misura 12 cm.
DATI
- A = 144 cm²
- DH = 6 cm
- B – b = 12 cm = D
b = ?
B =?
Dall’algebra sappiamo che, dati due numeri a e b, se conosciamo la loro somma
S = a + b
e la loro differenza
D = a – b
possiamo calcolarli facilmente applicando le formule seguenti:
Nel nostro caso, disponiamo della differenza tra le basi ma possiamo calcolare anche la loro somma. Sappiamo infatti che :
Abbiamo quindi :
(B + b) = 2A : h = (2 x 144) : 6 = 48 cm
Applicando le regole viste prima abbiamo:
- B = (48+12) : 2 = 30 cm
- b = (48 – 12) : 2 = 18 cm
AREA DEI POLIGONI : i triangoli
IL TRIANGOLO E’ UN POLIGONO CHE HA TRE LATI E TRE ANGOLI
Risulta:
A = (b x h) : 2
ESERCIZIO 1
In un triangolo rettangolo i cateti misurano 3 cm e 4 cm e la sua ipotenusa misura 5 cm. Calcola l’area e il perimetro del triangolo rettangolo.
RISOLUZIONE.
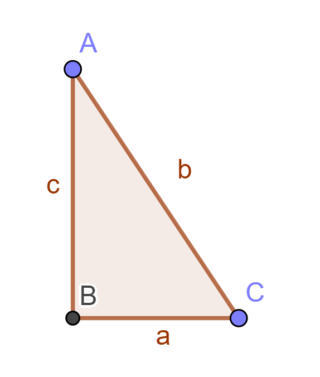Calcoliamo facilmente il perimetro come somma dei lati
P = a + b + c = 3+4+5 = 12 cm
Nel caso del triangolo rettangolo, inoltre, è facile anche calcolare l’area, come semiprodotto delle lunghezze dei cateti :
A = (a x c) : 2 = (3 x 4) : 2 = 6 cm2
ESERCIZIO 2
In un triangolo rettangolo di area 30 m2 uno dei due cateti misura 12 m e l’ipotenusa 13 m. Calcola il perimetro del triangolo rettangolo.
RISOLUZIONE
Per calcolare il perimetro ci serve la lunghezza del cateto mancante. Potremmo calcolarlo con il teorema di Pitagora ma, siccome ci viene fornita l’area della figura, possiamo ricavarlo facilmente dalla formula inversa.
a = 2A : c
In questo caso abbiamo :
a = (2 x 30) : 12 = 5 m
Possiamo quindi calcolare il perimetro :
P = a + b + c = 5 + 12 + 13 = 30 m
ESERCIZIO 3
Calcola la misura dei cateti di un triangolo rettangolo sapendo che questi sono uno il triplo dell’altro e che la misura dell’area del triangolo è di 96 cm².
DATI
b = 1/3 a
A = 96 cm²
- a = ?
- b = ?
SVOLGIMENTO
Se conosciamo il rapporto e il prodotto di due numeri, possiamo ricavarli facilmente. Infatti dire che il lato a è il triplo del lato b equivale a dire che il lato b è UN TERZO del lato a!
Quindi questo problema rientra nel “tipo”: prodotto di numeri, uno frazione dell’altro…
Sappiamo che l’area del triangolo è la metà dell’area di un rettangolo avente base ed altezza come quelli del triangolo dato. Mostriamo il rettangolo :
Siccome sappiamo che una dimensione è un terzo dell’altra, evidenziamo anche questo dato. Notiamo che il rettangolo risulta diviso in tre quadratini ( 3 x 1!). L’area di ciascun quadrato è UN TERZO dell’area del rettangolo. Possiamo così ricavare il suo lato.
Ci basta poi moltiplicare il valore ottenuto per 3 e ricavare la misura di a. Per calcolare b dobbiamo ovviamente moltiplicare il lato del quadrato per 1!
Svolgiamo i calcoli. Calcoliamo l’area del rettangolo, moltiplicando per 2 l’area del triangolo:
Arettang = 2 x 96 cm² = 192 cm²
Dividiamo ora quest’area per 3, in modo da avere l’area di ciascun quadratino:
A quadr = A rettang /3 = 192/3 = 64 cm²
𝓁quadr = √Aquadr = √64 = 8 cm
In questo caso, siccome b = 1/3 a, risulta :
b = 1 x 𝓁quadr = 8 cm
invece
a = 3 x 𝓁quadr= 24 cm
ESERCIZIO 4
Calcola l’area di un triangolo sapendo che la base e l’altezza ad essa relativa misurano rispettivamente 21 cm e 24 cm.
DATI
b = 21 cm
h = 24 cm
A = ?
SVOLGIMENTO
Siccome
A = (b x h) : 2
ci basta applicare la formula per risolvere il problema. Abbiamo infatti tutti i dati:
A = (21 x 24) : 2 = 252 cm²
ESERCIZIO 5
La somma della base e dell’altezza di un triangolo è 30 cm e la loro differenza è 6 cm. Calcola l’area.
DATI
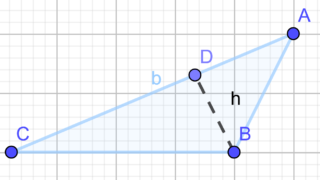b + h = 30 cm
b – h = 6 cm
A = ?
SVOLGIMENTO
Dall’algebra sappiamo che, dati due numeri a e b, se conosciamo la loro somma
S = a + b
e la loro differenza
D = a – b
possiamo calcolarli facilmente applicando le formule seguenti:
Nel nostro caso, abbiamo :
Possiamo ora calcolare la nostra area :
A = (b x h) : 2 = 108 cm²
ESERCIZIO 6
Calcola l’area di un triangolo avente i lati di 13, 14 e 15 cm (Erone).
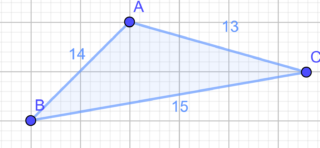
DATI
- a = 13 cm
- b = 14 cm
- c = 15 cm
A = ?
Sappiamo che la formula di Erone, il geniale matematico greco, ci permette di calcolare l’area di un triangolo qualsiasi, se conosciamo le misure dei suoi lati. Infatti:
Calcoliamo quindi il perimetro e poi applichiamo semplicemente la formula :
P = a + b+ c = 13 + 14 + 15 = 42 cm
p/2 = 42 : 2 = 21 cm
ESERCIZIO 7
Calcola l’altezza di un triangolo sapendo che la base m2isura 72 cm e che l’area misura 6084 cm².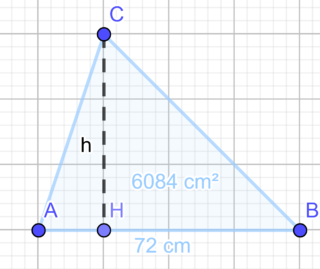
DATI :
A = 6084 cm²
b = 72 cm
h = ?
RISOLUZIONE
Siccome
A = (b x h) : 2
possiamo calcolare l’altezza applicando la formula inversa:
h = 2A : b
Con i dati numerici forniti, abbiamo :
h = 2 x 6084 : 72 = 169 cm
ESERCIZIO 8
In un triangolo isoscele la base misura 27 cm, i lati obliqui 22,5 cm e l’altezza è i 2/3 della base. Calcola la misura del perimetro e dell’area del triangolo.
DATI :
- b = 27 cm
- h = 2/3 b
- BC = AC = 22.5 cm
- P = ?
A = ?
SVOLGIMENTO
Calcoliamo immediatamente l’altezza :
h = 27 x 2/3 = 18 cm
Possiamo quindi calcolare facilmente perimetro ed area del triangolo isoscele:
P = b + 2AC = 27 + 22.5 x 2 = 72 cm
A = (b x h) : 2 = 243 cm²