DISTANZA DI UN PUNTO DA UNA RETTA

DISTANZA DI UN PUNTO DA UNA RETTA

Ultimo argomento legato al tema “piano cartesiano e retta”. Poi faremo un bel po’ di esercizi e finalmente passeremo ad altri argomenti. Spero sempre di riuscire a dedicarmi a più temi insieme, ma non mi riesce mai… Incrociamo le dita!

DISTANZA DI UN PUNTO DA UNA RETTA : definizione

Dalla Geometria sappiamo che

La distanza di un punto da una retta è la lunghezza del segmento che ha per estremi il punto stesso e il piede della perpendicolare condotta dal punto alla retta.

Ricordiamo poi che

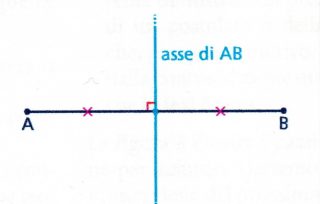
ASSE di un SEGMENTO è la retta perpendicolare ad un segmento e passante per il suo punto medio.

Di conseguenza, qualunque punto appartenente all’asse di un segmento ha uguale distanza dagli estremi del segmento. 

Torniamo alla distanza retta – punto.

Consideriamo una retta r ed un punto P, non appartenente alla retta r.

Conduciamo da P la perpendicolare alla retta data. Chiamiamo H il punto di intersezione fra la retta stessa e la perpendicolare.

La misura del segmento  PH rappresenta proprio la distanza del punto P dalla retta r.

In generale, la distanza di un punto P (x₀; y₀) da una retta di equazione ax+by+c= 0 è data dalla formula:

DISTANZA DI UN PUNTO DA UNA RETTA : ESEMPIO

Dato il punto P (2; 3) calcoliamo la sua distanza PH dalla retta di equazione

4x +3y – 5=0

Tracciamo da P le parallele agli assi fino a incontrare la retta data nei punti A e B.

Individuiamo così il triangolo rettangolo APB, di cui PH è l’altezza relativa all’ipotenusa.

Il punto A ha la stessa ordinata di P. Sostituendola nell’equazione della retta, possiamo determinare la sua ascissa:

4x +3∘(3) – 5=0

Ovvero: 4x = 5 – 9

E infine  x (A)= -1.

Il punto B, invece, ha la stessa ascissa di P per cui dall’equazione della retta, possiamo determinare la sua ordinata:

4∘ (2) +3 y – 5=0

ovvero : 3y = 5 – 8

e quindi y(B) = -1

Otteniamo quindi: A(-1; 3), B(2; -1).

Il doppio dell’area di APB si può ottenere moltiplicando le misure dei due cateti AP e PB. Se dividiamo poi per la misura dell’ipotenusa AB, otteniamo l’altezza PH relativa all’ipotenusa, ossia la misura cercata.

Siccome A e P  hanno la STESSA ORDINATA, la loro distanza è pari alla differenza tra le ascisse

AP = ∣x_P– x_A∣ = 3

Per PB, invece, siccome i due punti hanno la stessa ASCISSA, la loro distanza è pari alla differenza tra le ordinate:

PB = ∣y_B– y_P∣ = 4

Ovviamente AB è data dalla distanza tra due punti

Otteniamo quindi :

Applicando direttamente la formula vista sopra abbiamo:

• x₀ = 2
• y₀ = 3
• a = 4
• b = 3
• c = -5

che è il risultato ottenuto prima.

Domani ci dedicheremo ad un bel riassunto e poi a tanti esercizi!