Dopo aver “perso tempo” a vedere come si rappresentano sul piano cartesiano i punti e gli insiemi di punti, oggi torniamo a parlare delle rette e vediamo come si calcola la distanza tra due punti sul piano cartesiano.
Distanza fra due punti
Come possiamo calcolare la distanza tra due punti sul piano cartesiano? In pratica dobbiamo determinare la lunghezza del segmento che unisce i due punti. Per fare questo, dobbiamo distinguere TRE CASI
- i due punti hanno la STESSA ORDINATA⇒ AB parallelo asse x
- i due punti hanno la STESSA ASCISSA ⇒ AB parallelo asse y
- disposizione generica dei due punti ⇒ AB disposto in modo generico
CASO 1 : STESSA ORDINATA
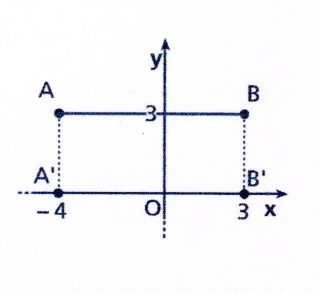Se due punti hanno la STESSA ORDINATA, significa che appartengono alla stessa retta parallela all’asse x, per cui la loro distanza è pari alla differenza tra le ascisse
AB = ∣xB– xA∣.
CASO 2 : STESSA ASCISSA
Se due punti hanno la STESSA ASCISSA, significa che appartengono alla stessa retta parallela all’asse y, per cui la loro distanza è pari alla differenza tra le ordinate:
AB = ∣yB– yA∣.
CASO 3 : PUNTI QUALSIASI DEL PIANO
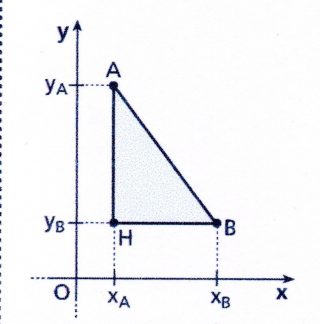Consideriamo un generico segmento AB, non parallelo agli assi. Per calcolare la lunghezza del segmento, dobbiamo applicare il teorema di Pitagora al triangolo rettangolo ABH, in cui i cateti sono due segmenti paralleli agli assi. il segmento AB, che unisce i due punti, rappresenta l’ipotenusa per cui abbiamo :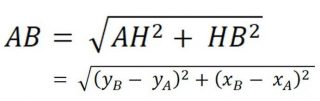
Distanza fra due punti : RICAPITOLANDO
DISTANZA TRA DUE PUNTI: ESERCIZI
Mettiamo in pratica quanto appreso con qualche esercizio
Intanto vi allego il pdf con teoria ed esercizi proposti. Spero di riuscire a postarvi anche le soluzioni quanto prima. Comunque alcuni degli esercizi proposti sono risolti
piano cartesiano distanza teoria ed esercizi
ESERCIZIO 1
Calcola la distanza tra due punti A(2; 6) e B (5; 10).
RISOLUZIONE
Rappresentiamo i punti dati sul piano cartesiano, per “visualizzare” la situazione.
Come possiamo notare, i due punti hanno ascissa e ordinata diverse, per cui ci troviamo nel CASO 3.
Dobbiamo quindi applicare la formula generale. Abbiamo :
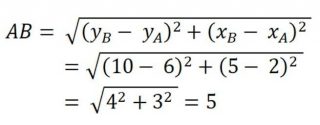
ESERCIZIO 2:
Calcola la distanza fra i punti indicati.
- A(2; 1), B(2; 6).
- A(3; 8) B (3; 19/2)
- A(- 4;4/3), B (-4; 7/2)
- A(- 4;- 4), B (1/2; -4)
- A(- 2; 0), B(8; 0).
- A(2; 5), B(5; 6)
- A(- 2;- 1), B(4; 12)
- A (- 3/4;4), B (17/4; 2)
- A(2;3/2), B(9; 31/2)
- A (1+√3, 2√3), B (1; +√3)
- A(2 +√2; 0), B(2; √7 )
- A (+√2 /3;3), B (0; 3+√2 /2)
ESERCIZIO 3
Determina il perimetro del triangolo i cui vertici sono A(2; 4), B(2; 1), C(6; 3).
RISOLUZIONE
Come sempre, innanzitutto individuiamo i tre punti dati sul piano cartesiano. Per calcolare il perimetro di qualsiasi figura geometrica dobbiamo SOMMARE le lunghezze dei suoi lati.
In questo caso, dobbiamo calcolare la lunghezza dei segmenti AB, AC e BC.
Per il segmento AB siamo nel CASO 1 e la sua lunghezza è pari al valore assoluto della differenza tra le ordinate dei due punti:
AB = 2
Per calcolare invece la lunghezza di AC e BC dobbiamo applicare la formula generale. Con i valori numerici dati abbiamo:
Per calcolare invece la lunghezza di AC e BC dobbiamo applicare la formula generale. Con i valori numerici dati abbiamo:
- AC = √17
- BC = 2√5
Il perimetro misura perciò
P= 2 + √17 + 2√5
ESERCIZIO 4
Calcola il perimetro del quadrilatero i cui vertici sono A(- 5; 6), B(0; 6), C(2; 2), D(- 3; – 3).
ESERCIZIO 5
Stabilisci se il triangolo ABC di vertici A(- 5; 6), B(- 1; 4), C(4; – 1) è isoscele.
Anche se dalla figura è evidente che i tre lati sondo diversi tra loro, dobbiamo controllare se AB è uguale a BC.
Calcoliamo la lunghezza dei due segmenti con la regola generale:
AB = 2√5
BC = 5√2
Calcoliamo anche AC = √130
I tre lati sono diversi e il triangolo è SCALENO
ESERCIZIO 6
Verifica che il triangolo di vertici A(- 3; 0), B(5; 0), C(1; 4√3) è equilatero.
ESERCIZIO 7
Verifica che il quadrilatero di vertici A(2; 1), B(8; 2), C(11; 7), D(5; 6) è un parallelogramma.
⇒ Dobbiamo verificare che i lati opposti siano congruenti
ESERCIZIO 8
Stabilisci se il triangolo ABC di vertici A(1; – 2), B(- 1; 2), C(- 1; – 3) è un triangolo rettangolo
è è sufficiente verificare se le misure dei lati soddisfano il teorema di Pitagora
ESERCIZIO 9
Determina il punto P sull’asse x equidistante da A(- 5; 5) e da B(0; 2).
ESERCIZIO 10
Individua il punto P che ha ordinata uguale all’ascissa ed è equidistante da A(- 2; 2) e B(5; 4).
Nel pdf allegato trovate molti altri esercizi