INSIEMI DI PUNTI E PIANO CARTESIANO

Dopo aver visto insieme come si rappresentano le coordinate di un punto nel sistema di riferimento cartesiano, oggi vediamo come possiamo rappresentare gli insiemi di punti.

Si tratta di una situazione che vi capiterà spesso in futuro, specie per rappresentare le soluzioni di disequazioni e di sistemi.

Conoscere come si rappresentano gli insiemi di punti nel piano cartesiano, in queste situazioni vi semplificherà parecchio i calcoli.

Vediamo come procedere con una serie di esercizi

INSIEMI DI PUNTI E PIANO CARTESIANO: esercizi

Vi mostro gli esercizi che troverete nel pdf allegato e di alcuni di essi vi illustro la soluzione. In un secondo pdf troverete poi le soluzioni complete. Gli esercizi sono tratti da Matematica blu di Bergamini & Co, edizione 2011.

Esercizio 1

In un riferimento cartesiano disegna :

l’insieme A dei punti (x; y) con ascissa x ≤2;
l’insieme B dei punti (x; y) con ordinata y ≥ 1;
l’insieme A ∩ B.

RISOLUZIONE

Tracciamo innanzitutto gli assi cartesiani e su di essi fissiamo un sistema di numerazione.

Disegniamo poi la retta parallela all’asse y, di equazione x=2 ed individuiamo l’insieme dei punti richiesto. Sono tutti quelli A SINISTRA della retta disegnata, che è COMPRESA nell’insieme.

Passiamo ora a disegnare la retta parallela all’asse x di equazione y=1. Disegniamo poi l’insieme dei punti di ORDINATA MAGGIORE O UGUALE a 1. Sono tutti quelli AL DI SOPRA della retta y=1, retta compresa.

L’insieme intersezione è quello in cui sono SODDISFATTE ENTRAMBE le diseguaglianze, dove quindi compaiono entrambi i colori. A ∩ B = {x≤2, y≥1}

Esercizio 2

In un riferimento cartesiano, A è l’insieme dei punti che hanno ascissa x ≥ 1, B è l’insieme dei punti che hanno ordinata y > 3. Disegna A ∩ B.

RISOLUZIONE

Come prima, disegniamo le due rette indicate, la prima parallela all’asse y e la seconda parallela all’asse x. L’insieme A è formato dai punti A DESTRA della retta x=1, che è COMPRESA nell’insieme.

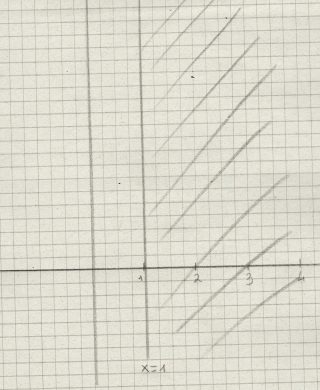
Analogamente, l’insieme B è formato dai punti AL DI SOPRA della retta y = 3, che NON è COMPRESA (è tratteggiata). L’insieme intersezione è formato dalla regione in cui i due insiemi SI SOVRAPPONGONO

Esercizio 3

In un riferimento cartesiano, A è l’insieme dei punti che hanno ascissa x tale che ∣x – 1∣ < 6 e B è l’insieme dei punti che hanno ordinata y tale che – 1 ≤ y < 8. Disegna A ∩ B.

RISOLUZIONE

Per disegnare l’insieme A, dobbiamo studiare il segno del valore assoluto.

Sappiamo che il valore assoluto di un’espressione coincide con l’espressione se questa è positiva o nulla, con il suo opposto se è negativa.

Nel nostro caso abbiamo

x – 1 ≥ 0 se x ≥ 1

Per x < 1, invece, il valore assoluto diventa

– x + 1

Dobbiamo quindi risolvere due disequazioni:

x-1 <6 è x <7 x ≥ 1

-x +1 <6 è -x < 5 è x >5 x < 1

L’insieme A è quindi rappresentato dalla striscia di piano compresa tra le rette di equazione x=5 e x=7, rette escluse

Disegniamo ora le due rette parallele all’asse x, di equazione y = -1 e y = 8, che individuano la striscia di piano dell’insieme B. La retta y = -1 è inclusa in B e per questo è a linea continua.

L’insieme intersezione è il rettangolo compreso tra le rette y= -1, y = 8, x = 5, x = 7

Esercizio 4

Dato il punto A = (√a-1; a/2 -1) trova per quali valori di a il punto è interno al quadrato che ha i lati paralleli agli assi cartesiani e ha due vertici di coordinate (-1; 0) e (3; 4).

Per la soluzione vedi il pdf allegato.

Esercizio 5

Calcola per quali valori di a il punto P(∣a + 1∣; a – 4) appartiene alla striscia individuata dalle parallele all’asse y passanti per A(-2; 0) e B(4; 0). [-5≤a ≤ 3]

Per la soluzione vedi il pdf allegato