EQUAZIONE DI UNA RETTA PER L’ORIGINE

EQUAZIONE DI UNA RETTA PER L’ORIGINE

Come abbiamo imparato già in passato, una retta è rappresentata matematicamente da un’equazione di primo grado in  due variabili.

Oggi vediamo che cosa significa quest’affermazione e vedremo come può presentarsi questa equazione nella sua forma più semplice. Riprenderemo certamente l’argomento molte volte, approfondendolo poco alla volta.

Intanto occupiamoci dell’equazione di una retta per l’origine degli assi  ma prima ricordiamoci che cosa si intende in Geometria con il termine “retta”. Vi ricordo che questi argomenti vi torneranno utili anche per Fisica, parlando del moto dei corpi. Vedremo presto perché

EQUAZIONE DI UNA RETTA PER L’ORIGINE: definizione di retta

Ricordiamo che geometricamente la retta è uno dei tre Enti Geometrici Fondamentali o Primitivi, insieme a punto e piano.

Una retta è una serie infinita di punti concatenati tra loro con la stessa direzione. Quindi è infinita e il suo spessore non è misurabile.

Le rette sono disegnate come segmenti i cui estremi sono tratteggiati e vengono contraddistinte da lettere minuscole dell’alfabeto.

ALCUNI POSTULATI

• Per due punti distinti passa una ed una sola retta
• Se due rette hanno due punti in comune esse coincidono
• Due rette che non hanno punti in comune sono parallele
• Due rette che hanno un punto in comune sono dette incidenti

EQUAZIONE DI UNA RETTA PER L’ORIGINE 

Nella sua forma generale, l’equazione di una retta passante per l’origine è del tipo:

y= mx

con m = y/x = coefficiente angolare.

Vedremo meglio che cosa rappresenta tra poco

EQUAZIONE DI UNA RETTA PER L’ORIGINE : LE BISETTRICI

Per m = 1 otteniamo l’equazione della BISETTRICE DEL PRIMO E TERZO QUADRANTE:

y = x

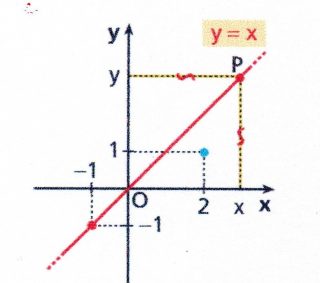Ogni punto della bisettrice è EQUIDISTANTE dagli assi cartesiani. In altre parole, tutti i punti della bisettrice hanno lo stesso valore per ascissa e ordinata. Come si vede nella figura a lato, il punto (-1;-1) appartiene alla bisettrice. Invece il punto di coordinate (2;1) non appartiene alla retta in esame.

Allo stesso modo, per m = – 1, otteniamo l’equazione della BISETTRICE DEL SECONDO E TERZO QUADRANTE:

 y = – x

I punti di questa retta hanno l’ascissa opposta all’ordinata. Ad esempio, appartengono a questa retta i punti di coordinate (-1; 1) e (2;-2):

EQUAZIONE DI UNA RETTA PER L’ORIGINE : il coefficiente angolare

Come abbiamo accennato poco prima, nell’equazione y = mx il numero m è chiamato coefficiente angolare. Esso esprime, per una retta passante per l’origine, il rapporto fra ordinata e ascissa di ogni punto della retta stessa, a eccezione dell’origine:

In generale, se x, y ≠ 0, possiamo scrivere :

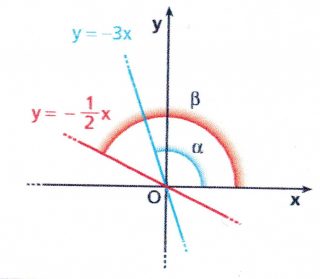
Il coefficiente angolare rappresenta l’angolo che la retta in esame forma con la semiretta positiva dell’asse x.  In particolare, se m >0, la retta forma con la semiretta positiva dell’asse x un angolo acuto;

Se m<0, il rapporto y/x è negativo: i punti della retta hanno coordinate discordi. Nel semipiano di ordinate positive la retta forma con la semiretta positiva dell’asse x un angolo ottuso:

EQUAZIONE DI UNA RETTA PER L’ORIGINE: le equazioni degli assi

Vediamo come ultima cosa quali sono le equazioni degli assi cartesiani.

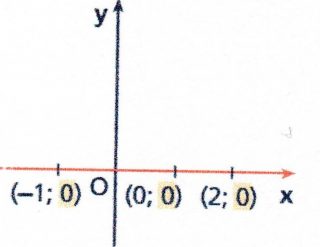Tutti i punti dell’asse x sono tali che la loro ordinata è 0. Di conseguenza, l’equazione dell’asse x è

y = 0

In modo analogo, tutti i punti dell’asse y hanno ascissa nulla. Quindi l’equazione dell’asse delle ordinate è

x = 0

Vediamo ora qualche esercizio sull’argomento

EQUAZIONE DI UNA RETTA PER L’ORIGINE : esercizi

Come al solito, vi propongo alcuni esercizi e poi li risolveremo insieme.

ESERCIZIO 1

Determina l’equazione della retta passante per l’origine e per il punto A(1/2; 2/5). Verifica poi se i punti

• B (5/4;1)
• C (2;5)

appartengono a tale retta.

SVOLGIMENTO

Siccome la retta passa per l’origine, la sua equazione sarà del tipo

y = mx.

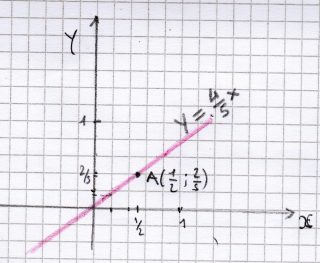Per poter scrivere l’equazione richiesta, quindi, dobbiamo calcolare il valore del coefficiente angolare. Siccome :

m = y/x

conoscendo le coordinate di un punto della retta possiamo calcolare m. Utilizzando le coordinate di A, otteniamo :

m = 2/5  : 1/2 = 2/5 ∘ 2 = 4/5

La retta richiesta è quindi :

y = 4/5 x

Verifichiamo ora se i punti B e C appartengono a tale retta. Per il punto B abbiamo :

y_B = 4/5 x_B

1 = 4/5 ∘ 5/4 ⇒ Il punto B appartiene alla retta trovata

Per il punto C abbiamo, invece :

y_C = 4/5 x_C

5 ≠ 4/5 ∘ 2 ⇒ Il punto C non appartiene alla nostra retta

ESERCIZIO 2

Scrivi l’equazione della retta, passante per l’origine e per il punto A. Verifica se il punto B appartiene alla retta trovata.

1. A (1/2;1) B (-1;-2) [y = 2x; si]
2.  A (1;- 1) B (-1/2;1/2) [y = – x; si]
3. A (- 2;0) B (-2; 5 ) [y = 0 ; NO]
4. A (3;2) B (6;4) [y = 2/3 x; si]

SVOLGIMENTO

Per ogni punto dato, ci basta calcolare il rapporto tra ordinata ed ascissa per determinare il coefficiente angolare e scrivere quindi l’equazione richiesta.

In seguito, per verificare se il punto B appartiene alla retta per A, possiamo procedere in due modi:

• sostituire nell’equazione trovata le coordinate del punto B per vedere se la soddisfano
• calcolare anche per B il valore del coefficiente angolare. Se è uguale a quello della retta data, allora B appartiene alla retta.

Per  il caso 1 abbiamo: A (1/2;1) B (-1;-2):

m = 1: ½ = 2 ⇒ la retta cercata è y = 2x

Per il punto B abbiamo m = (-2) : (-1) = 2 e quindi anche B appartiene alla retta per A

Sul pdf degli esercizi trovate la soluzione completa.

ESERCIZIO 3 

I seguenti gruppi di punti appartengono tutti ad una stessa retta passante per l’origine, tranne uno. Scrivi l’equazione della retta e individua il punto estraneo.

• A (-1; -5)  B (2;10) C(5;10) D (3;15)
• A (-3; 9)  B (-2; 6) C(2;-6) D (1;3)

ESERCIZIO 4 

Scrivi l’equazione della retta passante per l’origine avente il coefficiente angolare indicato e disegna la retta.

• m = 2
• m = – 2.
• m = 3;
• m = – 3.
• m = 1/3
• m = -1/3

EQUAZIONE DI UNA RETTA PER ORIGINE : il pdf con la teoria

 esercizi con soluzioni