FRAZIONI IN BREVE
Come vi ho accennato in precedenza, in questo periodo mi sto dedicando ad aiutare i miei ragazzi con il ripasso di diversi argomenti, che, trattati in maniera forse frettolosa e poco approfondita nel corso del difficile anno scolastico che stanno vivendo, non hanno “sedimentato” nel loro cervello.
Dopo aver rivisto equazioni e i primi cenni di calcolo letterale, nei prossimi giorni ci dedicheremo ai numeri razionali, per passare poi ai radicali e alle disequazioni. Torneremo alla geometria analitica e a numerosi altri argomenti, sempre cercando di dedicarci più alla teoria che alla pratica.
Intanto riprendiamo i concetti che sono alla base dei numeri razionali.
FRAZIONI IN BREVE
Come per rendere sempre possibili la sottrazione abbiamo introdotto i numeri relativi interi, così per rendere sempre possibile la divisione introduciamo i NUMERI RAZIONALI, che si indicano con ℚ. Ne parleremo meglio prossimamente. Intanto però ricordiamo intanto che cos’è una FRAZIONE
FRAZIONI IN BREVE : che cos’è una frazione
Una frazione è il quoziente fra due numeri interi a e b, con a e b appartenenti all’insieme ℤ e b ≠ 0. La frazione si scrive:
dove a è il numeratore e b è il denominatore. Se numeratore e denominatore hanno lo stesso segno la frazione è positiva, se hanno segno discorde la frazione è negativa.
Una frazione a/b , con a, b∊N, b ≠ 0, è:
- propria se 0 < a < b. Una frazione propria è quindi minore di 1
- apparente se a è multiplo di b. Essa in realtà rappresenta un numero INTERO
- impropria se a > b e a non è multiplo di b. E’ quindi maggiore di 1
Dalla definizione si deduce che:

FRAZIONI IN BREVE : frazioni equivalenti
Due frazioni

sono equivalenti e si scrive:

se risulta:
a · d = b · c
ovvero se il prodotto del numeratore della prima per il denominatore della seconda è uguale al prodotto del denominatore della prima per il numeratore della seconda.
Per stabilire se due frazioni sono equivalenti, quindi, ci basta eseguire i prodotti “IN CROCE” e vedere se sono uguali.
PROPRIETÀ INVARIANTIVA
moltiplicando, o dividendo, numeratore o denominatore di una frazione per un numero diverso da zero, si ha una frazione equivalente:
FRAZIONI IN BREVE : RIDURRE UNA FRAZIONE AI MINIMI TERMINI
Data una frazione, quando applichiamo la proprietà invariantiva dividendo numeratore e denominatore per uno stesso numero, diciamo che semplifichiamo la frazione.
Se dividiamo NUMERATORE e DENOMINATORE per il loro M.C.D., otteniamo una frazione in cui numeratore e denominatore non hanno più divisori in comune diversi da 1, ovvero se sono primi tra loro.
Una frazione a/b si dice irriducibile o ridotta ai minimi termini se a e b sono primi fra loro. Per ridurre una frazione ai minimi termini si applica la proprietà invariantiva dividendo numeratore e denominatore per il M.C.D.
CONFRONTO TRA FRAZIONI
⇨ FRAZIONI CON UGUALE DENOMINATORE:
Se due frazioni hanno lo stesso denominatore, è MAGGIORE quella con numeratore più grande:
5/9 > 2>9
⇨ FRAZIONI CON UGUALE NUMERATORE:
Se due frazioni hanno lo stesso numeratore, è MAGGIORE quella con denominatore più piccolo:
3/7 > 3/11
⇨ CASO GENERALE
IN GENERALE, se numeratore e denominatore sono diversi, dobbiamo RIDURRE le frazioni allo stesso denominatore. Come? Calcolando in minimo denominatore comune, ovvero il m.c.m. dei denominatori 〈m.c.d.〉.
Possiamo però semplificare le operazioni se abbiamo due sole frazioni. In questo caso, possiamo ricorrere ai PRODOTTI IN CROCE. Risulta perciò:

NOTA BENE: Anche nel caso di FRAZIONI NEGATIVE la regola resta valida, attribuendo il segno negativo ai numeratori. Se per esempio dobbiamo confrontare
 ci basta scrivere :
ci basta scrivere :

Effettuando il prodotto in croce otteniamo (-7) e (-10). Siccome (-7) > (-10) abbiamo:

FRAZIONI IN BREVE: LE OPERAZIONI CON LE FRAZIONI
⇒ ADDIZIONE E SOTTRAZIONE TRA FRAZIONI :
Date due frazioni aventi lo stesso denominatore, la somma si esegue riscrivendo lo stesso denominatore e mettendo al numeratore la somma algebrica dei numeratori
Se le due frazioni a/b e c/d hanno DIVERSO DENOMINATORE, dobbiamo effettuare la riduzione al minimo comune denominatore m.c.d., cioè dobbiamo calcolare il minimo comune multiplo fra i denominatori. Abbiamo quindi 
RICORDA: L’opposto di a/b è -a/b:

da cui si deduce che la somma di due opposti è uguale a zero: 
⇒ MOLTIPLICAZIONE TRA FRAZIONI
Dobbiamo moltiplicare i numeratori tra loro e i denominatori tra loro:

Se un numeratore e un denominatore, della stessa frazione o di frazioni diverse, hanno qualche fattore in comune, ci conviene SEMPLIFICARE PRIMA di eseguire la moltiplicazione, per avere calcoli con numeri più piccoli.
⇒ FRAZIONE RECIPROCA o INVERSA
Il reciproco di a/b è la frazione INVERSA b/a, ottenuta scambiando numeratore e denominatore:
 In pratica ci basta “ribaltare” la frazione di partenza per ottenere il suo reciproco.
In pratica ci basta “ribaltare” la frazione di partenza per ottenere il suo reciproco.
Si deduce che :

⇒ DIVISIONE TRA FRAZIONI
Per dividere due frazioni, moltiplichiamo la prima per la reciproca della seconda:

Per eseguire le operazioni si adottano le stesse regole viste per le operazioni di base.
⇒ Elevamento a potenza
La potenza n-esima di un numero razionale , a/b, con n ∈ ℕ e n > 0, si ottiene elevando alla stessa potenza numeratore e denominatore :
Le proprietà delle potenze sono le stesse viste in precedenza e valgono anche le stesse regole relative ai segni viste in Z.
⇒ POTENZA CON ESPONENTE INTERO NEGATIVO
Avendo introdotto il concetto di reciproco di una frazione, possiamo ampliare anche il concetto di potenza, considerando la potenza n-esima di un numero relativo a ≠ 0 con esponente intero negativo: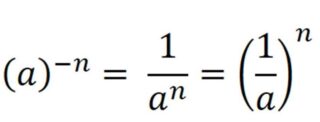
La potenza di un numero razionale, diverso da 0, con esponente intero negativo è una potenza che ha per base il reciproco del numero dato e per esponente l’opposto dell’esponente
Nel prossimo articolo vedremo come dalle frazioni possiamo passare ai numeri decimali e viceversa. Troverete poi tanti esercizi!