Dopo aver rivisto le operazioni con le frazioni ed altri concetti base, prima di passare a parlare dei NUMERI RAZIONALI, grazie a cui è possibile sempre effettuare la divisione, oggi ripassiamo un altro concetto fondamentale della matematica, la scrittura delle frazioni sotto forma di numero decimale. E poi vedremo anche come effettuare il procedimento inverso.
DA FRAZIONE A NUMERO DECIMALE : I Numeri decimali
Ricordiamo che
NUMERO DECIMALE è una successione di cifre separate da una virgola:
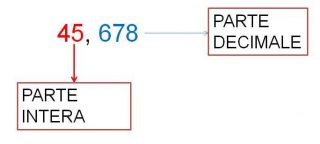
La parte a SINISTRA della virgola si chiama PARTE INTERA mentre quella a DESTRA prende il nome di PARTE DECIMALE.
Come sappiamo, possiamo sempre scrivere una frazione sotto forma di numero decimale, cioè di numero con la virgola. Ci basta infatti eseguire la DIVISIONE tra numeratore e denominatore.
Il quoziente ottenuto può essere:
- un numero intero se il numeratore è multiplo del denominatore;
- un numero decimale finito, cioè un numero che presenta dopo la virgola un numero finito di cifre;
- un numero decimale illimitato periodico (chiamato semplicemente numero periodico), cioè un numero che ha INFINITE CIFRE dopo la virgola. Da una certa posizione in poi, queste cifre SI RIPETONO a gruppi uguali. Il gruppo di cifre che si ripete è il PERIODO e viene indicato con un trattino soprassegnato.
FRAZIONI DECIMALI
Una frazione che ha come denominatore una potenza di 10, con esponente maggiore di zero, si chiama frazione decimale, e il numero decimale corrispondente si ottiene spostando a sinistra la virgola:
- d/10 = 0,d
- c/100= 0,0c
- m/1000 = 0,00m
Sappiamo inoltre che una frazione con denominatore uguale a 100 può essere espressa utilizzando la notazione percentuale (con simbolo %, che significa ×1/100).
STABILIRE IL TIPO DI NUMERO GENERATO DA UNA FRAZIONE
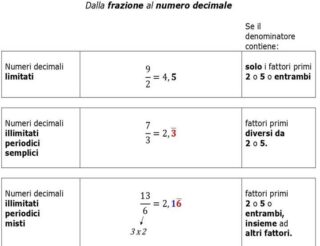
Possiamo stabilire il tipo di numero che genera una frazione senza dovere effettuare la divisione tra numeratore e denominatore. Infatti la rappresentazione decimale della frazione DIPENDE dai FATTORI che compaiono al denominatore, scomposto in fattori primi.
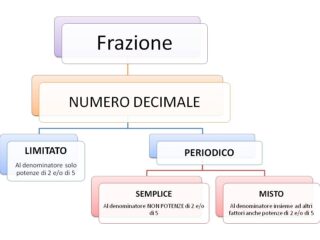
⇒ Una frazione ridotta ai minimi termini genera un numero decimale FINITO se al denominatore compaiono SOLO potenze di 2 e di 5.
![]()
⇒ Quando i fattori primi del denominatore di una frazione (ridotta ai minimi termini) NON sono potenze di 2 e di 5, il risultato è un numero decimale ILLIMITATO PERIODICO SEMPLICE, ovvero un numero che dopo la virgola presenta un gruppo di cifre, dette periodo, che si ripetono indefinitamente. Il periodo si scrive una sola volta soprassegnato:

⇒ Quando i fattori primi del denominatore di una frazione (ridotta ai minimi termini) comprendono ALTRI fattori oltre a potenze di 2 e/o di 5, il risultato è un numero decimale ILLIMITATO PERIODICO MISTO, in cui tra la virgola e il periodo è compreso un gruppo di cifre detto antiperiodo: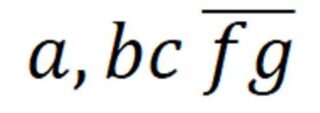
![]()
Altri esempi:
![]()
![]()

RICAPITOLANDO
Un numero decimale è la somma della sua parte intera con frazioni che hanno le cifre decimali per numeratori e potenze di 10 per denominatori.

Data una frazione, possiamo trasformarla in un numero decimale dividendo il numeratore per il denominatore.
Se nella divisione otteniamo un resto uguale a zero, il numero è decimale finito.
45/120 = 0,375
Se non c’è un resto uguale a zero, i resti sono tuttavia sempre minori del divisore, quindi, prima o poi, incontreremo di nuovo lo stesso resto e otterremo le stesse cifre decimali.
Quando il numero non è decimale finito, ha cifre che si ripetono periodicamente: il numero è decimale periodico. Chiamiamo periodo il gruppo di cifre che si ripete.
Un numero decimale periodico è:
- semplice se le cifre si ripetono subito dopo la virgola ⇒ al denominatore NON compaiono i fattori 2 e/o 5;
- misto se le cifre si ripetono non sono subito dopo la virgola. Chiamiamo antiperiodo il gruppo di cifre decimali tra la virgola e il periodo ⇒ al denominatore compaiono ALTRI FATTORI oltre a 2 e/o 5.
DA NUMERO DECIMALE A FRAZIONE
Vediamo ora come effettuare il procedimento inverso, cioè come trasformare un numero decimale in una frazione, detta FRAZIONE GENERATRICE.
Infatti, dato un numero decimale, finito o periodico, possiamo sempre trasformarlo in una frazione.
⇒ Se il numero decimale è FINITO, la frazione generatrice è ottenuta scrivendo al numeratore il numero e al denominatore la cifra 1 seguita da tanti zeri quante sono le cifre decimali:
0,a = a/10
0,0b = b/100
Una volta compiuta la trasformazione, se necessario, possiamo ridurre la frazione ai minimi termini, semplificandola.
⇒ La frazione generatrice di un numero decimale PERIODICO è una frazione che ha :
- numeratore uguale alla differenza tra il numero scritto senza la virgola e il numero costituito da tutte le cifre (intere e decimali) che precedono le cifre del periodo;
- denominatore formato da tanti NOVE quante sono le cifre del periodo e tanti ZERI quante sono le cifre dell’ANTIPERIODO:
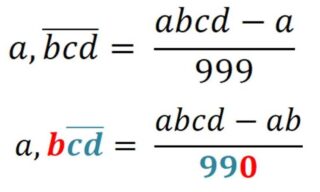
Ad esempio:


RICAPITOLANDO


DA FRAZIONE A NUMERO DECIMALE E RITORNO: GLI ESERCIZI
Come al solito, vi allego il pdf con la lezione in versione stampabile e poi troverete anche una serie di schemi “riassuntivi”, oltre ad esercizi sugli argomenti trattati. Domani ci occuperemo dei numeri razionali e parleremo anche di come approssimare un numero decimale