RETTA PASSANTE PER DUE PUNTI
Coraggio, ragazzi, siamo quasi alla fine dell’argomento “retta e piano cartesiano”, che ho deciso di svolgere con particolare attenzione, vista la sua importanza non solo per il corso di matematica. Infatti vi servirà anche per tutte le altre materie scientifiche, come avremo modo di vedere tra brevissimo!
Oggi vediamo insieme come scrivere l’equazione di una generica retta passante per due punti del piano cartesiano e poi parleremo di rette perpendicolari e paralleli.
RETTA PASSANTE PER DUE PUNTI : come ricavarla
Dalla condizione di allineamento, sappiamo che, dati due punti DISTINTI del piano, per essi passa UNA ED UNA SOLA RETTA.
Questo significa che, date le coordinate di due punti, possiamo determinare l’equazione della retta che li unisce.
 Prendiamo due punti qualsiasi, punti P1 (x1; y1) e P2 (x2; y2). Dobbiamo calcolare l’equazione della retta che passa per essi e per il generico punto P (x;y)
Prendiamo due punti qualsiasi, punti P1 (x1; y1) e P2 (x2; y2). Dobbiamo calcolare l’equazione della retta che passa per essi e per il generico punto P (x;y)
Possiamo calcolare il suo coefficiente angolare:

Per ogni punto P(x;y) della retta, deve essere valida la condizione di allineamento:
y – y1 = m(x – x1)
Come vedremo meglio a breve, questo significa che la retta cercata appartiene al fascio di rette proprio passante per P.
Sostituendo ad m l’espressione trovata, otteniamo:

Dividendo quindi entrambi i membri dell’equazione per y2– y1, otteniamo
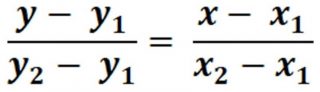
che è appunto l’equazione della retta passante per i punti dati.
RETTA PASSANTE PER UN PUNTO e di coefficiente angolare noto.
Se invece di conoscere i due punti, conosciamo le coordinate di un punto e il coefficiente angolare, dobbiamo scrivere l’equazione nella forma

ovvero :
y – y1 = m(x – x1)
Ci basta quindi sostituire in quest’equazione i valori forniti per ricavare la retta cercata.
Esercitiamoci ora con la relazione
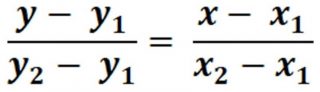
che tanto utile vi tornerà anche in futuro.
RETTA PASSANTE PER DUE PUNTI. Esempio
Calcoliamo l’equazione della retta passante per i punti
A (-1;3) e B (-4;2).
Controlliamo innanzi tutto che i due punti non appartengano ad una stessa retta parallela ad uno degli assi. Siccome :
xA≠ xB
yA≠ yB
possiamo applicare la formula precedente. Otteniamo quindi

ovvero:

Svolgiamo ora i calcoli per riportare l’equazione alla forma esplicita:
-(y-3) = -1/3 (x+1)
Cambiamo di segno ai due membri dell’equazione, ottenendo
y – 3 = 1/3 (x+1)
Spostiamo ora a destra del segno di uguale (-3):
y = 1/3 x + 1/3 +3
Infine, sommando i termini noti, otteniamo l’equazione cercata, della retta passante per A e B:
 (FORMA ESPLICITA)
(FORMA ESPLICITA)
Vogliamo riportarla alla forma implicita. Moltiplichiamo entrambi i membri dell’equazione per 3 e trasportiamo tutti i termini a sinistra del segno di uguaglianza. Otteniamo:
-x + 3y -10 = 0
(FORMA IMPLICITA)
ovvero l’equazione in forma implicita.
Il fine settimana sarà tutto dedicato agli esercizi sull’argomento “retta” e poi passeremo ad occuparci di sistemi lineari!