NUMERI NATURALI dalle operazioni alle espressioni

NUMERI NATURALI per il primo superiore

Anche se ne abbiamo già parlato, torniamo ad approfondire l’argomento, per riassumere un po’ e riprendere le file anche per i miei ragazzi del primo anno delle superiori.

Nel pdf allegato trovate la versione stampabile con gli esercizi. Come sempre, vi allegherò anche il file con le soluzioni

NUMERI NATURALI  : definizione

Sono i numeri che conosciamo dalla nascita: 

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …

Indichiamo il loro insieme con ℕ.

I numeri naturali possono essere rappresentati su una semiretta orientata, cioè una semiretta sulla quale segniamo con una freccia il verso di percorrenza.

All’origine facciamo corrispondere il numero 0. La rappresentazione sulla semiretta fa vedere che l’insieme dei numeri naturali è ordinato e possiamo sempre confrontare due numeri naturali fra loro.

 

⇒ RELAZIONI DI ORDINE:

• < minore
• > maggiore
• ≥ maggiore o uguale
• ≤ minore o uguale

NUMERI NATURALI : LE OPERAZIONI IN ℕ

Con i numeri naturali si eseguono le operazioni di ADDIZIONE, SOTTRAZIONE, MOLTIPLICAZIONE E DIVISIONE.

Come potete vedere dalla tabella precedente, i due numeri con i quali si opera, cioè gli operandi, assumono nomi particolari, così come i risultati delle operazioni.

⇒ Nell’addizione il primo e il secondo operando sono gli addendi, il risultato è la somma o totale

⇒ Nella sottrazione il primo operando è il minuendo, il secondo operando è il sottraendo, il risultato è la differenza.

 

⇒  Per la moltiplicazione, invece, il primo e il secondo operando sono i fattori, il risultato è il prodotto.

⇒ Nel caso della divisione il primo operando prende il nome di dividendo, il secondo operando è il divisore, il risultato è il quoziente

RICORDA:

• Addizione e moltiplicazione sono OPERAZIONI INTERNE ad ℕ. Ovvero: il risultato di tali operazioni è ancora un numero naturale.
• La sottrazione è l’operazione INVERSA dell’addizione
• La divisione è l’operazione INVERSA della moltiplicazione
• Lo ZERO è l’elemento NEUTRO della SOMMA :

n + 0 = 0 + n = n  qualunque sia il numero n ∈ ℕ

• Il numero 1 è l’elemento NEUTRO della MOLTIPLICAZIONE:

n ∘ 1 = 1 ∘ n = n  qualunque sia il numero n ∈ ℕ

NUMERI NATURALI: le proprietà delle operazioni

Per comodità, vi indico le proprietà e le operazioni a cui si riferiscono. Per saperne di più, fate riferimento alle varie operazioni:

• addizione 
• sottrazione
• moltiplicazione
• divisione

Le operazioni in N godono delle seguenti proprietà:

⇒ ASSOCIATIVA : 

• ADDIZIONE :  (a+b) + c = b + (a + c)  a + (b+c)
• MOLTIPLICAZIONE : (a ∘ b) ∘ c = a ∘ (b ∘ c) = b ∘ (a ∘ c)

⇒COMMUTATIVA :

• ADDIZIONE :  a+b = b + a 
• MOLTIPLICAZIONE : a ∘ b  = b ∘ a 

⇒ INVARIANTIVA 

• SOTTRAZIONE : il risultato non cambia se aggiungiamo o togliamo uno stesso numero sia al minuendo che al sottraendo
• DIVISIONE: il risultato non cambia se moltiplichiamo o dividiamo per uno stesso numero, diverso da zero, sia il dividendo che il divisore

⇒ DISTRIBUTIVA RISPETTO ALLA SOMMA E ALLA DIFFERENZA

• MOLTIPLICAZIONE
  • RISPETTO ALLA SOMMA :  a ∘ (b+c) = a ∘ b + a ∘ c
  • RISPETTO ALLA DIFFERENZA : a ∘ (b-c) = a ∘ b – a ∘ c
• DIVISIONE
  • RISPETTO ALLA SOMMA :  (a + b) : c = a : c + b : c
  • RISPETTO ALLA DIFFERENZA : (b-c) : a =  b : a –  c : a

RICAPITOLANDO: 

NUMERI NATURALI : la potenza

In ℕ è possibile anche l’ELEVAMENTO A POTENZA

Ricordiamo che le potenze sono moltiplicazioni particolari, nelle quali tutti i fattori sono uguali: 

2⁷ (si legge «2 alla settima») = 2 x 2 x 2 x 2 x 2 x 2 x 2

Il numero 2 è la base e il numero 7 è l’esponente della potenza.

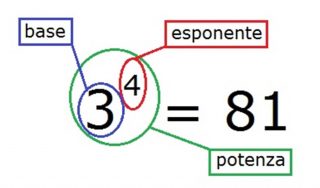
La base indica quale fattore viene moltiplicato per se stesso, l’esponente indica il numero di fattori uguali.

Ricorda : 

•  aⁿ = a ∘ a ∘ a ∘ a …. ∘ a se n > 1;
• a⁰ = 1 se a ≠ 0;
•  a¹ = a
• NON HA SIGNIFICATO LA SCRITTURA 0⁰ (ZERO ELEVATO A ZERO non esiste!) 

PROPRIETÀ DELLE POTENZE

1) Prodotto di potenze con la stessa base: Il prodotto di potenze con la stessa base è una potenza che ha la stessa base e come esponente la somma degli esponenti.

a^m ∘ aⁿ = a ^m+n

Ad esempio : 5³ ∘ 5⁴ = 5 ³⁺⁴ = 5⁷

2) Quoziente di potenze con la stessa base: Il quoziente di potenze con la stessa base è una potenza che ha la stessa base e come esponente la differenza degli esponenti.

a^m : aⁿ = a ^m–n,  con a≠ 0 e n ≤ m

Ad esempio : 7⁹ : 7⁴ = 7 ^9-4 = 7 ^9-4

3) Potenza di potenza: La potenza di una potenza è una potenza che ha la stessa base e per esponente il prodotto degli esponenti.

(a^m)ⁿ = a ^{m∘ n}

Ad esempio  (6²)⁵ = 6 ^{2∘ 5}

4) Prodotto di potenze con lo stesso esponente : Il prodotto di potenze con lo stesso esponente è una potenza che ha lo stesso esponente e come base il prodotto delle basi.

a^m ∘ b^m = (a ∘ b)^m

Ad esempio  3²∘  2² = (3∘ 2) ²= (6) ² = 36

5) Quoziente di potenze con lo stesso esponente :Il quoziente di potenze con lo stesso esponente è una potenza che ha lo stesso esponente e come base il quoziente delle basi.

a^m : b^m = (a : b)^m

Ad esempio  6²: 2² = (6:2) ²= (3) ² = 9

ESPRESSIONI CON I NUMERI NATURALI

Un’espressione è semplicemente una sequenza di operazioni, da eseguire rispettando le REGOLE DI PRIORITÀ:

• prima vengono calcolate le potenze,
• poi le moltiplicazioni e le divisioni, nell’ordine in cui sono scritte,
• infine le addizioni e le sottrazioni, sempre nell’ordine in cui sono scritte.

Le parentesi CAMBIANO la priorità delle operazioni. In altre parole: le PARENTESI MODIFICANO l’ordine con cui devono essere svolte le operazioni.

RICORDA: prima i calcoli presenti all’interno delle parentesi tonde, poi quelli all’interno delle quadre e infine quelli all’interno delle graffe. Sempre rispettando le regole di priorità viste prima.

NUMERI NATURALI : MULTIPLI, DIVISORI, M.C.D., m.c.m.

Consideriamo i numeri naturali a e b. Se esiste un numero naturale q tale che a = b x q, diciamo che:

• a è multiplo di b;
• b è divisore di a.

Ad esempio : 10 = 2 x 5. Diciamo che

• 10 è un multiplo di 2 e 5
• 2 e 5 sono i DIVISORI di 10

il MULTIPLO di un numero è tale se la divisione tra il multiplo ed il numero stesso ha RESTO ZERO

Per ottenere i multipli di un numero, ci basta moltiplicare tale numero per 0,1,2….

I MULTIPLI DI UN NUMERO SONO INFINITI

Chiamiamo invece DIVISORE di un numero quello in cui la divisione tra un numero qualsiasi e il numero dato ha resto ZERO

I DIVISORI SONO FINITI

CRITERI DI DIVISIBILITA’

Ricordiamo insieme i criteri di divisibilità più utilizzati

• per 2 

Un numero è divisibile per 2 se l’ultima cifra è PARI (0 – 2 – 4 – 6 -8)

• PER 5

Un numero è divisibile per 5 se l’ultima cifra è 0 oppure 5

• PER 3

la somma delle cifre è divisibile per 3 

• PER 4 

le ultime due cifre a destra del numero sono 00 oppure un multiplo di 4

• per 25 

Le ultime due cifre del numero sono 25, 50, 75 oppure 00

• PER 9 

La somma delle cifre del numero è divisibile per 9

• PER 11 

LA somma delle cifre di posto pari e di quelle di posto dispari ha come differenza ZERO oppure un multiplo di 11 

SCOMPOSIZIONE IN FATTORI PRIMI

Se un numero non è un numero primo, possiamo scriverlo come PRODOTTO DI NUMERI PRIMI. Il processo si chiama “SCOMPOSIZIONE IN FATTORI PRIMI”. 

La scomposizione di un numero in fattori primi viene anche chiamata fattorizzazione in numeri primi. Tale operazione è utile per calcolare il Massimo Comune Divisore e il Minimo Comune Multiplo tra due o più numeri

MASSIMO COMUNE DIVISORE

Fra due o più numeri naturali diversi da 0,il massimo comune divisore (MCD) è il più grande fra i loro divisori comuni

⇒ REGOLA : Se scomponiamo in fattori primi due o più numeri naturali, il MCD è il prodotto dei fattori comuni, presi una sola volta, con l’esponente minore.

MINIMO COMUNE MULTIPLO

Fra due o più numeri naturali diversi da 0, il minimo comune multiplo (mcm) è il più piccolo fra i loro multipli comuni diversi da 0.

⇒REGOLA  : Se scomponiamo in fattori primi due o più numeri naturali, il mcm è il prodotto di tutti i fattori comuni e non comuni, presi una sola volta, con l’esponente maggiore.

Ricorda:

Se due numeri non hanno fattori in comune diversi da 1, diciamo che sono primi tra loro e risulta

• M. C.D. = 1
• m.c.m. = il prodotto dei due numeri.

Ad esempio : 10 e 21 sono primi tra loro. Risulta quindi :

• M.C.D. (10,21)= 1
• m.c.m. (10,21)= 10 ∘ 21 = 210

COMPLETA la seguente tabella applicando i criteri di divisibilità.

a è divisibile per	2	3	5	10	11	25
45
60
171
506
1625
2304
4950
5400

Scrivi le espressioni relative alle seguenti frasi e calcolane il risultato.

• Sottrarre 9 dal prodotto di 8 per 2.
• Moltiplicare per 3 la differenza tra 12 e 7.
• Dividere 15 per la differenza tra 9 e 4 e poi sommare 2.
• Moltiplicare 3 per la somma di 9 e del quoziente di 14 e 2.
• Sottrarre 3 al risultato della divisione di 12 per la differenza tra 5 e 1.
• Dividere 18 per la differenza tra 9 e il prodotto di 3 per 2.
• Sottrarre a 17 la differenza tra il prodotto di 8 per 2 e 9.
• Dividere per 5 la differenza tra 15 e il prodotto di 5 per 2.
• Moltiplicare per 7 la differenza tra 10 e 8; sottrarre al risultato 14

Scrivi le espressioni che forniscono le soluzioni dei seguenti problemi e calcolane i valori.

• Anna riceve dalla madre 8 euro e va ad acquistare 2 scatole di colori del costo di 3 euro l’una. Al ritorno si ferma dalla nonna che le regala 5 euro. Con quanto denaro arriva a casa Anna? [7 euro]
• Luca e suo fratello Andrea vanno al cinema ricevendo 10 euro ciascuno dai genitori. Il costo di un biglietto è di 5 euro; Luca acquista prima di entrare al cinema una bibita del costo di 2 euro, mentre Andrea compera 2 pacchetti di patatine da 2 euro l’uno: complessivamente con quanto denaro tornano a casa i due fratelli? [4 euro]
• Una cuoca possiede 4 sacchetti di farina del peso di 1 kg ciascuno. Deve fare 7 dolci: nei primi 3 occorrono 350 g di farina per ciascuno e negli altri, 600 g di farina per ciascuno. Alla fine quanta farina rimane alla cuoca? [550 g]
• Una nonna ha 5 nipotini e 25 torroncini. Decide di dare 3 torroncini al primo nipotino e uno in più a ciascuno degli altri nipotini. Quanti torroncini le rimangono? [6]
• In uno stabilimento tessile, in una settimana (6 giorni lavorativi), si producono 26 304 m di tela. La tela viene suddivisa in pezze da 32 m ciascuna. Quanti giorni lavorativi occorrono per fabbricare 1233 pezze?                                    [9]

 Le espressioni con le quattro operazioni

[12-(3+2)]∘2-[(2+3)∘2-4+(3+1) ∘ 2-5+1]                                                               [4]

{[10∘(3+2)]:[16+3∘3]}+3∘ (2+1)                                                                             [11]

[20 : (3 ∘2-2)+4] : (6-3 ∘ 2+3)

{[12+2∘ (3+1)] :(3+2)}-(3+1)                                                                                  [0]

{12 ∘ [(5+2) ∘ 3-19]} : [(3+1) ∘ (2+1)]                                                                    [2]

{15-[13+(2+14) : (2+2∘3)-3]} : [(2+7) : 3]                                                  [1]

{(2+7-3∘2) ∘ [4- (1+2)]}: [4-(2 ∘ 2-1)]                                                                     [3]

{[(10-7+3+2-5) ∘ (25:5)-2] ∘ [(30-5+1-16) : (30 : 15)+10+7-20]} : 2                [13]

13-{8 ∘ 15-[(7 ∘ 5+5) : 8+20 : (28 : 4-3)]} : 11                                                      [3]

(22-5 ∘ 4) : 2+{[36 : 2+7 ∘ 3-1- (2 ∘ 8+6)]-2³}                                                       [9]

(2⁰ ∘ 3⁰+8) : 3+[3²-(2¹+4) : 2]+ (2⁴+2) :  3²                                                           [11]

 [(4+3²-1) : 2²+45 : 3²] : 2²+(21 ∘ 3) : 9+1⁰                                                                              [10]

{[(3²+11) : 2²]² : 5-1} ∘ 2³-[7² : (2 ∘3+1)+2³+10⁰]                                     [16]

{[(6⁰+2 ∘ 5²-11) : 2³+ 8]-2⁰} : 4+(7-4) ∘ 2+ 3² ∘ 2                                     [27]

[(243 : 81+4³ : 4-3) : (5-3⁰)+125 : 25] ∘ 2² : 3                                          [12]

numeri naturali esercizi CON SOLUZIONI